2020 CCPC 秦皇岛 虚拟参赛 暨 补题
基地加入的比较晚, 第一次训练没参加, 这是第二次训练
记录
第一题开A, 签到, 蒋叶桢7minAC.
我继续找题面短的题翻译, 找到G, 简单的枚举题, 蒋叶桢有一点点小小的细节一开始没处理好, 不过在蒋叶桢和张炀杰的讨论下还是很快AC了, 41min.
同时我开了E, 在一边想, 蒋叶桢交完G开了F, 我E有思路了, 和张炀杰交流了一下, 感觉没啥问题, 于是就开始码. 一开始没想太清晰, 打完后发现最后的处理错了. 这时一共交了2发. 蒋叶桢和张炀杰在1h50minAC了F, 蒋叶桢马上来支援我, 发现问题所在, 同时找到了一个重要性质, 提出了一个树状数组维护, 我发现单调性, 于是蒋叶桢给我打了个优先队列维护的补丁, 还是WA了.
之后我一直在找"逻辑错误"的小细节, 看到一处可能出问题的地方就改一处, 改完就交. 交了N发E, 还是WA, 甚至写了线段树维护, 依旧WA. 同时张炀杰开了K, 和蒋叶桢讨论无果, 蒋叶桢开了I. 于是我们各自一题一直在写.
我实在调不出E了, 于是去膜拜蒋叶桢. 蒋叶桢之前对着I苦思冥想到了将向量拆解的思路, 用gcd更新向量, 用exgcd求是否有解, 我写了最后一步的方程给他(他一开始没想到这个方程), 他想出了后续写法, 并且认为能AC, 但是也不知道为什么一直WA.
然后去膜拜张炀杰. 张炀杰手玩出了几个性质, 想出了贪心的算法, 但是被我Hack了, 然后他就基本放弃写K了.
至此结束, E WA了9发, I WA了3发
总结
打得很不理想, 该写出来的E, I, K都没有写出来, 以及我们甚至题都没开完.
总结一下, 我们需要注意:
- 优先开题, 找签到题
- 注意数据范围, 不要爆int (E)
- 证明算法准确性再写 (K)
补题
A. A Greeting from Qinhuangdao
$T$组测试, $r$个红气球, $b$个蓝气球, 求从中选出两个红气球的方案数. 答案以最简分数形式输出.
$1 \le T \le 10, 1 \le r, b \le 100$
签到题
组合数学, 很显然答案为
$$\frac{ \tbinom{r}{2} }{ \tbinom{r+b}{2} } = \frac{ r(r+1) }{ (r+b)(r+b-1) }$$
下面处理分数. 分子分母约去最大公因数即可 设$p = r(r+1), q = (r+b)(r+b-1), g = gcd(p, q)$, 那么约分后的分子, 分母分别为 $p’ = \frac{p}{g}, q’ = \frac{q}{g}$
复杂度$O(1)$
int t, r, b;
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d%d", &r, &b);
int p = r * (r - 1);
int q = (r + b) * (r + b - 1);
int g = __gcd(p, q);
p /= g, q/= g;
printf("Case #%d: %d/%d\n", kase, p, q);
}
return 0;
}B. Bounding Wall
$T$组测试. 给出$n \times m$的$01$矩阵$M$. $q$次操作.
1 x y将矩阵中$(x, y)$取反2 x y表示查询查询如下:
找一个面积最大的矩形边框(平行与坐标轴), 满足:
- 边框上的点都是$0$
- $(x, y)$在边框上
$1 \le T, n, m, q \le 10^3$
先来看询问.
首先很容易发现, 我们可以枚举$(x, y)$在矩阵的哪一条边上, 这样只需要做$4$次同样的算法即可.
下面仅仅考虑$(x, y)$在下边的做法.
通过$O(n^2)$的预处理, 可以很快知道$(x, y)$左右两边最近的$1$. 设为$L$和$R$
然后考虑枚举上边所在的行$u$. 现在只需要知道两根竖直边在哪一列上即可. $j$列能够作为竖直边的充要条件是$j \in (L, R), \forall i \in [u, x], M_{i, j} = 0$. 显然要使面积最大, 应该要让左竖直边的下标$j_l$尽量小, 右竖直边的下标$j_r$尽量大.
对于一个$1$, 只要他行$(u, x]$中, 他的行号其实是不重要的. 如果$i(i \in[u, x])$行在$(L, R)$之间出现了$1$, 我们其实可以直接认为这个$1$在$u+1$行. 一种考虑方式是尝试从大到小枚举$u$, 让$u+1$以下的行的信息"压"到$u+1$上, 如下图:
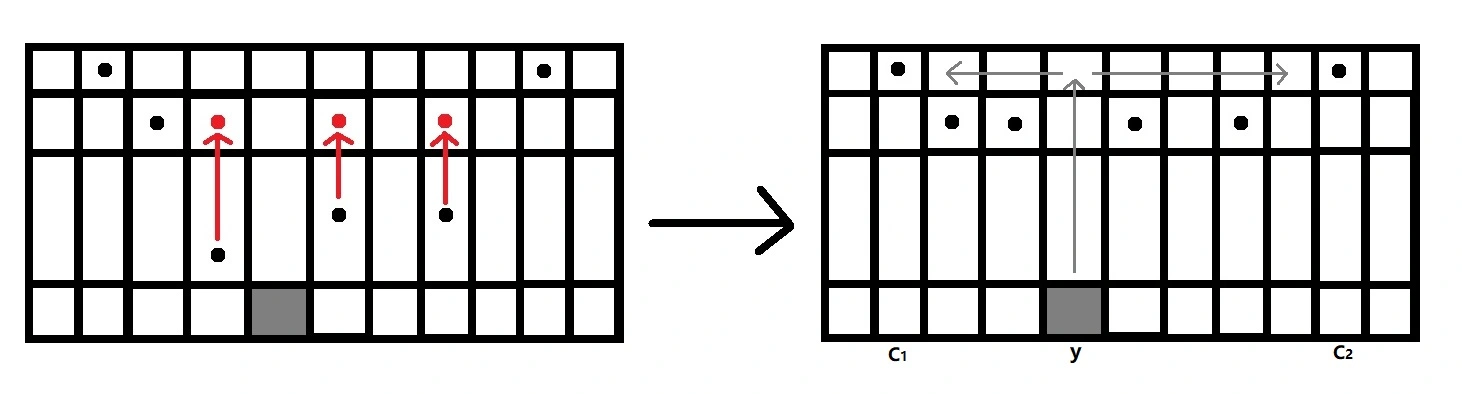
然后在$u$行找左右两边最近的$1$, 见上图(右), 然后看$u+1$行对应的左右位置, 如果是$0$(右图右箭头下方), 那么就找到了一侧的竖直边, 上图即$c_2$; 如果是$1$(右图左箭头下方), 那么还得找$u+1$行$c_1 + 1$所在"连通块"的最右端(或最左端, 看情况)
“连通块"都出来了, 还不知道用并查集吗? 并查集维护一下每个连通块最左边和最右边的点的下标即可, 详见代码.
不过, 我们不能直接枚举每行的$1$, 否则复杂度会是$O(n^2)$, 加上查询总复杂度有$O(n^3)$, 过不了.
从大到小做的话, 可以发现, 如果一列上有多个$1$, 只需考虑低的$1$即可. 可以在$O(n^2)$内预处理出在$(x, y)$上方离$(x, y)$最近的$1$的位置. 只考虑这些$1$, 就可以在$O(n + m) = O(n)$的时间完成了.
具体来说, 对每一行开一个池子(vector) pool[] , 对于每一个在$(L, R)$中的$j$, 快速查询到$(x, j)$点上方的$1$的行号$i$, 然后把$j$压入pool[i]. 当枚举到$i$行的时候, 把 pool[i] 中的$j$拿出来处理就行.
到这里, 询问的关键算法就结束了. 复杂度$O(n^2)$
然后需要把矩阵旋转$3$次, 每一次跑一遍, 答案取最大即可.
但是! 不能"在线"旋转, 否则每查询一次, 都要花$O(n^2)$的时间旋转, 这样总复杂度就是$O(n^3)$了. 可以离线, 即对每个方向的矩阵跑一遍所有询问, 记录答案. 转了以后重新跑一遍所有询问, 更新答案. 这样总共只需要转$3$下, 旋转的复杂度$O(n^2)$不会加在询问$O(n)$上.
注意旋转了以后, 操作中的$(x, y)$也需要旋转到相应的点$(x’, y’)$上
每次旋转了以后, 也可以用$O(n^2)$的时间重新预处理数组l[][], r[][], up[][]了.
最后看简单一点的修改.
矩阵中的值直接取反, 一个点的值改变, 只会改变$x’$行的l[][], r[][]和$y’$列的up[][], 直接花$O(n)$重新处理该行或列即可.
总复杂度$O(n^2)$
const int maxn = 1e3+10;
struct Question {
int op, x, y;
};
int t, n, m, q, N, M;
char str[maxn][maxn];
int layout[maxn][maxn], ans[maxn];
int l[maxn][maxn], r[maxn][maxn], up[maxn][maxn];
int fa[maxn], mark[maxn], mx[maxn], mn[maxn];
vector<int> pool[maxn];
vector<Question> qs;
void UpdAns(int id, int a) {
ans[id] = max(ans[id], a);
}
int Find(int x) {
return x == fa[x] ? x : fa[x] = Find(fa[x]);
}
void Union(int x, int y) {
x = Find(x), y = Find(y);
fa[x] = y;
mn[y] = min(mn[y], mn[x]);
mx[y] = max(mx[y], mx[x]);
}
void sol(int id, int rot) {
int op = qs[id].op, x = qs[id].x, y = qs[id].y;
if (rot == 1) {
int xx = x, yy = y;
x = yy, y = N - xx + 1;
}
else if (rot == 2) {
x = N - x + 1, y = M - y + 1;
}
else if (rot == 3) {
int xx = x, yy = y;
x = M - yy + 1, y = xx;
}
if (op == 1) {
layout[x][y] ^= 1;
//只需要维护当前行或者列的值
for (int j = 1; j <= m; j++)
l[x][j] = layout[x][j] ? j : l[x][j-1];
for (int j = m; j; j--)
r[x][j] = layout[x][j] ? j : r[x][j+1];
for (int i = 1; i <= n; i++)
up[i][y] = layout[i][y] ? i : up[i-1][y];
}
else {
if (!layout[x][y]) {
//L, R是最左, 最右的不可放置点
int L = l[x][y], R = r[x][y];
UpdAns(id, R - L - 1);
//清空pool
for (int i = 1; i < x; i++)
pool[i].clear();
//计算pool, 初始化fa, mark
for (int j = L + 1; j <= R - 1; j++)
pool[up[x][j]].push_back(j);
for (int j = L; j <= R; j++) {
mark[j] = 0;
fa[j] = mn[j] = mx[j] = j;
}
mark[L] = mark[R] = 1;
//枚举上边
for (int i = x - 1; i; i--) {
//更新并查集, 加入当前行的不可放置点
for (auto j : pool[i]) if (!mark[j]) {
mark[j] = 1;
if (mark[j-1])
Union(j, j-1);
if (mark[j+1])
Union(j, j+1);
}
int cur_L = max(L, l[i][y]);
cur_L = Find(cur_L);
cur_L = mx[cur_L];
int cur_R = min(R, r[i][y]);
cur_R = Find(cur_R);
cur_R = mn[cur_R];
if (cur_L < y && y < cur_R)
UpdAns(id, (cur_R - cur_L - 1) * (x - i + 1));
}
}
}
}
//初始化l, r, up
void Init() {
for (int i = 1; i <= n; i++) {
l[i][0] = 0;
for (int j = 1; j <= m; j++)
l[i][j] = layout[i][j] ? j : l[i][j-1];
}
for (int i = 1; i <= n; i++) {
r[i][m+1] = m+1;
for (int j = m; j; j--)
r[i][j] = layout[i][j] ? j : r[i][j+1];
}
for (int j = 1; j <= m; j++) {
up[0][j] = 0;
for (int i = 1; i <= n; i++)
up[i][j] = layout[i][j] ? i : up[i-1][j];
}
}
//旋转layout
void Rotate(int rot) {
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++) {
if (rot == 1)
layout[j][N - i + 1] = str[i][j] == '.';
else if (rot == 2)
layout[N - i + 1][M - j + 1] = str[i][j] == '.';
else if (rot == 3)
layout[M - j + 1][i] = str[i][j] == '.';
}
swap(n, m);
}
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d%d%d", &n, &m, &q);
N = n, M = m;
for (int i = 1; i <= n; i++)
scanf("%s", str[i] + 1);
qs.clear();
for (int qq = 1; qq <= q; qq++) {
int op, x, y;
scanf("%d%d%d", &op, &x, &y);
qs.push_back(Question{op, x, y});
}
int sz = qs.size();
for (int i = 0; i < sz; i++)
ans[i] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
layout[i][j] = str[i][j] == '.';
Init();
for (int i = 0; i < sz; i++)
sol(i, 0);
for (int cnt = 1; cnt <= 3; cnt++) {
Rotate(cnt);
Init();
for (int i = 0; i < sz; i++)
sol(i, cnt);
}
printf("Case #%d:\n", kase);
for (int i = 0; i < sz; i++) if (qs[i].op == 2)
printf("%d\n", ans[i]);
}
return 0;
}E. Exam Results
$T$组测试. $n$个学生参加考试. 如果第$i$个学生发挥得好, 他可以得$a_i$分; 否则他只能得$b_i$分. 一场考试结束后, 设最高分为$x$, 及格线为$x \cdot p$%. 问可能最多有几个学生及格.
$1 \le T \le 5 \cdot 10^3, 1 \le n \le 2 \cdot 10^5, 1 \le p \le 100, 1 \le b_i \le a_i \le 10^9$
法一(vp时想的): 枚举 + 二分查找 + 线段树
考虑枚举最高分, 便可通过二分查找来找到及格线左右的人数, $O(nlogn)$能过.
枚举最高分的时候, 应该对分数进行从大到小的顺序排序, 然后依次考虑, 考虑过的分数是不能选的.
那么既然要枚举最高分, 那么一定得把$n$个学生"拆"开, 一共$2n$个分数. 这样才可以枚举最高分.
每个学生都至少需要一个分数, 所以一但在枚举的过程中发现同一个学生的两个分数都枚举过了, 那么直接结束, 即枚举完第一个出现的$b$结束.
二分查找, 可以找到及格线左右的分数. 设当前枚举位置为$i$, 及格线位置为$pos$. 考虑在及格线以上的分数, 他们被分为了两个部分:
- 已经枚举过的分数, 即$[1, i)$
- 还没有枚举到的分数(和正在枚举的分数), 即$[i, pos]$.
已经枚举过的不应该选, 否则当前枚举的最高分就不是最高. 有效区间为$[i, pos]$, 即需要算$[i, pos]$中有多少个学生. 可以用线段树维护每个$a$或$b$对应的下标, 然后查询区间不为$0$的个数.
这样的做法很蠢. 复杂度$O(nlog^2 n)$
法二: 枚举 + 滑动窗口
枚举同理, 我们需要维护$[i, pos]$中学生的个数. 注意到$x$和$x \cdot p$% 都是单调的, 那么只需要维护一个滑动窗口即可. 具体来说: 维护一个数组 vis[] , 表示学生在窗口内出现的次数. 和 tot , 表示窗口内学生总数.
- 尾指针拓展一个分数时, 找到对应的学生, 记录次数(
vis[tail]++). 如果是第一次找到这学生( 修改前的vis[tail] == 0), 则窗口内学生总数加一(tot++). 不断拓展尾指针, 直到他不在及格线内(score[tail] < score[head] * p / 100). - 头指针移除时, 找到对应学生, 减去次数(
vis[head]--), 同理维护tot.
复杂度$O(n)$
最后注意score[head] * p / 100, $a(b)$ 最大可为$10^9$, $p$最大为$100$, 直接乘就炸int啦!!!
我才不会告诉你因为这个细节vp时调了3个小时换了2种做法WA了9发, 而且当场还没一个人找到这个极其**的失误
const int maxn = 2e5+10;
int t, n, p;
int a[maxn], b[maxn], vis[maxn];
struct Score {
int num, flag, id;
bool operator < (const Score &N) const {
return num == N.num ? flag < N.flag : num > N.num;
}
} score[maxn * 2];
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d%d", &n, &p);
int ans = 0;
for (int i = 1; i <= n; i++) {
scanf("%d%d", a + i, b + i);
score[i] = Score{a[i], 0, i};
score[i + n] = Score{b[i], 1, i};
vis[i] = 0;
}
sort(score + 1, score + 1 + 2 * n);
int tot = 0, tail = 1;
for (int head = 1; head <= 2 * n; head++) {
while (score[tail].num >= score[head].num * (p / 100.0)) {
int id = score[tail].id;
if (vis[id] == 0)
tot++;
vis[id]++;
tail++;
}
ans = max(ans, tot);
if (score[head].flag)
break;
int id = score[head].id;
if (vis[id] == 1)
tot--;
vis[id]--;
}
printf("Case #%d: %d\n", kase, ans);
}
return 0;
}F. Friendly Group
$T$组测试. 给出一张$n$个点$m$条边的图$G = <V, E>$(注意图不一定连通), 求一个子图$G’ = <V’, E’>$(可以是$\emptyset$), 使得$|E’| - |V’|$最大. 输出最大值.
$1 \le T \le 10^4, 1 \le n \le 3 \dots 10^5, 1 \le m \le 10^6$
首先有这样的一个性质: 如果选了一颗树, 则答案会-1, 不优.
考虑一个$n$个点$n$条边的连通块, 他的贡献就刚好是$0$, 如果全选上, 那么不会使答案减小. 下面考虑选该连通块的某一个子图, 如果选到的是一颗树, 由上述性质可得不优. 不如不选; 如果选到的还是一个$m$个点$m$条边的连通块, 那么可选可不选. 不会有其他情况. 那么该连通块及其所有子图的贡献都不会大于$0$
所以我们得到这样一个策略:
- 如果一个连通块的边数小于等于点数, 则不选;
- 如果一个连通块的边数大于点数, 则选上这一整个连通块.
具体做法只要维护并查集, 多开一个 edge[] 表示有多少条边, 合并的时候更新 edge[] 即可
复杂度$O(n\alpha(n))$
const int maxn = 3e5+10;
int t, n, m, fa[maxn], size[maxn], edge[maxn], vis[maxn];
void Init() {
for (int i = 1; i <= n; i++) {
fa[i] = i;
size[i] = 1;
edge[i] = 0;
vis[i] = 0;
}
}
int Find(int x) {
return fa[x] == x ? x : fa[x] = Find(fa[x]);
}
void Union(int x, int y) {
x = Find(x), y = Find(y);
if (x != y) {
fa[x] = y;
size[y] += size[x];
edge[y] += edge[x] + 1;
}
else
edge[y]++;
}
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
int ans = 0;
scanf("%d%d", &n, &m);
Init();
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d%d", &x, &y);
Union(x, y);
}
for (int i = 1; i <= n; i++) {
if (!vis[Find(i)]) {
ans += max(0, edge[Find(i)] - size[Find(i)]);
vis[Find(i)] = 1;
}
}
printf("Case #%d: %d\n", kase, ans);
}
return 0;
}G. Good Number
$T$组测试. 一个正数$x$被称为"好数"的充要条件为
$$\lfloor \sqrt[k]{x} \rfloor \mid x$$
其中$k$是给出的正整数. $T$次询问, $[1, n]$中有多少个"好数”.
$1 \le T \le 10, 1 \le n, k \le 10^9$
当$k = 1$时, 显然所有的数都是"好数", 直接输出$n$即可.
当$k = 2$时, 我们发现$\lfloor \sqrt[k]{x} \rfloor$ 的个数为$O(\sqrt{10^9}) = O(10^{4.5})$, 可以尝试枚举. 而$k \ge 2$时, 这个个数会更小, 所以枚举因子, 尝试计算因子的贡献.
枚举$i = \lfloor \sqrt[k]{x} \rfloor$, 先去掉取整, 变形就可以算得最小的$x$, 设为$x_i$, $x_i = i^k$, 还能得到最大的$x$, 就是$x_{i+1} - 1$, 即$(i+1)^k - 1$.
找到可能是$i$的倍数的所有数(即区间$[x_i, x_{i+1})$内的所有数)之后, 我们考虑到底哪些数是$i$的倍数, 或者说, 区间里有多少个数是$i$的倍数. 由于相邻"倍数"的间隔是固定的, 且为$i$, 比如$i = 3$, 那么$3, 6, 9…$都是$3$的倍数, 他们间隔为$3$. 而恰好区间的第一个数就是$i$的倍数, 那么实际上求的个数就是能把区间$[x_i, x_{i-1})$分成多少份长度为$i$的小区间, 最后一个小区间可能长度并不是$i$(比$i$小), 但是他也算贡献, 因为该小区间的第一个数是$i$的倍数. 至此, $i$的贡献就能够求出来了, 即
$$\lceil \frac{ x_{i+1} - x_i }{i} \rceil$$
处理$x_{i+1}$的时候要判断一下是否大于$n+1$, 如果大于了$n+1$, 则取$n+1$, 这样恰好减去$x_i$就是区间$[x_i, n]$的长度.
需要注意的是, $k$很大, 算$i^k$时会炸, 需要在 Power() 里判断一下中间答案是否超过了$n$, 如果超过了, 说明$i^k$一定超过$n$, 根据上述说明, 返回$n+1$即可.
复杂度小于等于$O(\sqrt{n})$
int t, n, k;
LL power(LL a, LL b) {
LL res = 1;
while (b) {
if (b&1)
res *= a;
if (a > (LL)n || res > (LL)n)
return INTINF;
a *= a;
b >>= 1;
}
return res;
}
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d%d", &n, &k);
if (k == 1) {
printf("Case #%d: %d\n", kase, n);
continue;
}
int last = 1, ans = 0;
for (int m = 1; power(m, k) <= (LL)n; m++) {
LL r = power(m+1, k);
ans += ((min(r, (LL)(n+1)) - last) + m - 1) / m;
last = r;
}
printf("Case #%d: %d\n", kase, ans);
}
return 0;
}H. Holy Sequence
对于一个长度为$n$的正整数数列$a_n$, 他合法的条件是:
- $\forall i \in [1, n], a_i \in {1, 2, \dots, n}$;
- $\forall i \in [1, n], p_i - p_{i-1} \le 1 (p_k = max \{ a_1, a_2, \dots, a_k \}, p_0 = 0)$.
对于每一个 $t = 1, 2, \dots, n$, 求
$$\sum_{A \in S_n}cnt(A, t)^2$$
其中, $S_n$是所有长度为$n$的合法序列的集合, $cnt(A, t)$是$t$在数列$A$> 中出现的次数.
答案对$m$取模.
$T$组测试, 给出$n, m$
$1 \le T \le 10, 1 \le n \le 3000, 1 \le m \le 10^9$
感谢zzs, 舍友书名号, 大佬jyz, 我终于理解了这道数数题.
直接求显然不合理, 我们需要从平方的组合意义上"拆贡献".
首先考虑$x^2$代表什么. 比如小明有$x$个数, 分别为$1, 2, \dots n$, 小红也有同样的$x$个数. 两人分别出一个数, 有序配对, 有多少中配对方法. 这个答案就是$x^2$.
这里只不过反过来, 把$x^2$拆成配对数, 如下:
$$cnt(A, t)^2 = \Big| \{ \left \langle i, j \right \rangle \mid a_i = a_j = t, 1 \le i, j \le n \} \Big|$$
所以有:
$$ \begin{aligned} &\sum_{A \in S_n}cnt(A, t)^2 \\ = &\sum_{A \in S_n}\Big| \{ \langle i, j \rangle \mid a_i = a_j = t, 1 \le i, j \le n \} \Big| \end{aligned} $$
这算的是"所有合法序列$A$中, 满足条件$a_i = a_j = t$的有序对$\langle i, j \rangle $有多少个". 可以转化成"对于满足条件$a_i = a_j = t$的所有有序对$\langle i, j \rangle$, 有多少个合法序列$A$"
即:
$$ \begin{aligned} &\sum_{A \in S_n} cnt(A, t)^2 \\ = &\sum_{A \in S_n} \Big| \{ \langle i, j \rangle \mid a_i = a_j = t, 1 \le i, j \le n \} \Big| \\ = &\sum_{1 \le i, j \le n} \Big| \{ A \in S_n \mid a_i = a_j = t \} \Big| \end{aligned} $$
计算有序对数量时, 如果$i \ne j$, 那么有序对数量可以用无序对数量乘以$2$表示; 如果$i=j$, 有序无序是一样的东西. 所以, 上述式子进一步可以写成:
$$ \begin{aligned} &\sum_{A \in S_n} cnt(A, t)^2 \\ = &\sum_{A \in S_n} \Big| \{ \langle i, j \rangle \mid a_i = a_j = t, 1 \le i, j \le n \} \Big| \\ = &\sum_{1 \le i, j \le n} \Big| \{ A \in S_n \mid a_i = a_j = t \} \Big| \\ = &\sum_{1 \le i < j \le n} 2 \cdot \Big| \{ A \in S_n \mid a_i = a_j = t \} \Big| + \sum_{1 \le i \le n} \Big| \{ A \in S_n \mid a_i = t \} \Big| \\ = &\sum_{1 \le i \le n} \Big| \{ A \in S_n \mid a_i = t \} \Big| + 2 \sum_{1 \le i < j \le n} \Big| \{ A \in S_n \mid a_i = a_j = t \} \Big| \end{aligned} $$
先来看如何求$\sum_{1 \le i \le n} \Big| \{ A \in S_n \mid a_i = t \} \Big|$.
枚举$i, a_i = t$, 只要能够快速知道合法的前缀和后缀各有多少, 然后相乘即可. 可以用$dp$求合法前缀和后缀. 设$f(i, j)$为最大值为$j$的长度为$i$的合法序列数量, 方程:
$$f(i, j) = j \cdot f(i-1, j) + f(i-1, j-1)$$
解释如下:
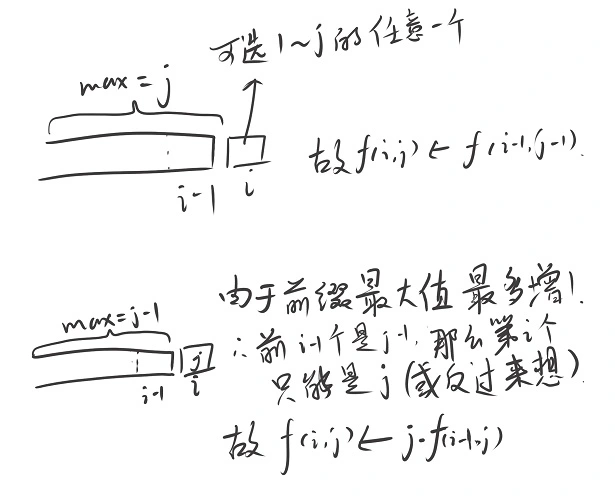
设$g(i, j)$为(强行)**$a_1 = j$**时, 前缀最大值增加不超过$1$, 长度为$i$的合法序列数量.
为什么要这么定义呢? 因为已经枚举了$a_i = t$, 后面的序列也满足前缀最大增加量不超过$1$, 首先得把$t$考虑进来, 然后还要考虑后面有多少个数. 这样的定义是没问题的. 难点在于方程转移:
$$g(i, j) = j \cdot g(i-1, j) + g(i-1, j+1)$$
解释如下:
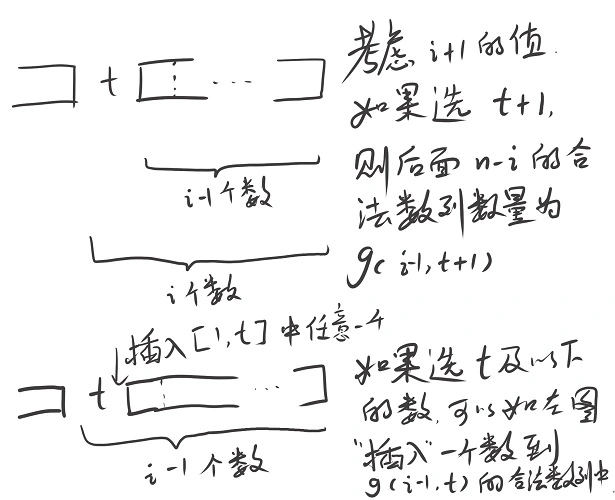
枚举$t$第一次出现的位置$i$, 选择两个$t$配对, 有下面这些情况:
- 选的两个$t$相同, 都是$a_i$, 贡献为$f(i-1, t-1) \cdot g(n - i + 1, t)$
- 选的两个$t$不同, 第一个是$a_i$, 第二个是后面某一个$a_j = t$, 贡献为$2 \cdot f(i-1, t-1) \cdot (n-i)g(n-i, t)$(还是插入法, 在$n-1$个元素的合法后缀之间插入一个$t$, 就相当于"枚举"到了这个$a_j = t$, 有序, 乘以$2$)
- 选的两个$t$相同, 是后面某一个$a_j = t$, 贡献为$f(i-1, t-1) \cdot (n-1) \cdot g(n-i, t)$
- 选的两个$t$不同, 都在$i$后面, 贡献为$2 \cdot \tbinom{n-i}{2} f(i-1, t-1) \cdot g(n-i-1, t)$
注意到$a_i = t$的一个必要条件是$t \le i$, 在推$f$和$g$的时候需要注意.
边界条件很简单, 略.
还需注意, 在枚举$i$的过程中, 如果后面的个数不足, 则不能转移.
复杂度$O(n^2)$
const int maxn = 3e3+10;
int t, n, P;
LL Plus(LL a, LL b) {
return a + b >= P ? (a + b) % P : a + b;
}
LL Mult(LL a, LL b) {
return a * b >= P ? a * b % P : a * b;
}
LL f[maxn][maxn], g[maxn][maxn], ans[maxn];
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d%d", &n, &P);
memset(f, 0, sizeof(f));
memset(g, 0, sizeof(g));
memset(ans, 0, sizeof(ans));
f[0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
f[i][j] = Plus(f[i-1][j-1], Mult(j, f[i-1][j]));
for (int j = 1; j <= n; j++)
g[1][j] = 1;
for (int i = 2; i <= n; i++)
for (int j = (n - i + 1); j; j--)
g[i][j] = Plus(g[i-1][j+1], Mult(j, g[i-1][j]));
// 对每个t, 枚举其第一次出现的位置i, 由**题目**可知i >= t
for (int t = 1; t <= n; t++)
for (int i = t; i <= n; i++) {
// 两次选i这个位置的t
ans[t] = Plus(ans[t], Mult(f[i-1][t-1], g[n-i+1][t]));
// 第一次选i这个位置的t, 第二次选后面某一个t
// 由于有序, 所以乘以2
if (i < n)
ans[t] = Plus(ans[t], Mult(Mult(2, f[i-1][t-1]), Mult(n-i, g[n-i][t])));
// 两次选后面同一个t
if (i < n)
ans[t] = Plus(ans[t], Mult(f[i-1][t-1], Mult(n-i, g[n-i][t])));
// 两次选后面不同的t
if (i + 1 < n)
ans[t] = Plus(ans[t], Mult(Mult(f[i-1][t-1], n-i), Mult(n-i-1, g[n-i-1][t])));
}
printf("Case #%d:\n", kase);
for (int t = 1; t <= n; t++)
printf("%lld ", ans[t]);
puts("");
}
return 0;
}J. Jewel Splitting
$T$组测试. 给出一个小写字母组成的字符串, 设其长度为$n$. 把这个字符串切成若干小段, 每小段$d$个字符(如果$d$整除$n$, 则有$\frac{n}{d}$段; 否则会有一段不满$d$的), 考虑这$\lfloor \frac{n}{d} \rfloor$个长度为$d$的小段, 将其排成一个长为$\lfloor \frac{n}{d} \rfloor$, 宽为$d$的矩阵. 对于每个$d \in [1, n]$, 问能够排出多少个不同的矩阵. 答案对$998244353$取模
$1 \le T \le 10^3, 1 \le |s| \le 3 \cdot 10^5$
首先$d$不同矩阵肯定不同. 考虑某一个确定的$d$.
由组合数学的知识可以知道, 对于$x = \lfloor \frac{n}{d} \rfloor$行, 字符串为$s_k$的行有$x_k$个, 那么不同的矩阵的个数为$\frac{x!}{\Pi x_k!}$. 对字符串进行哈希, 就可以取一个特定子串, 统计其出现的次数了.
难点在于, $n \mod d \ne 0$时, 能够得到的$\lfloor \frac{n}{d} \rfloor$个子段可能与之前考虑过的某一些子段是相同的, 不能重复计算. 所以我们还得对子段的集合进行判重, 这里又得用一个哈希.
因为子段已经具有了哈希值, 我们可以对子段的哈希值离散化, 然后用这些子段的哈希值的离散化值进行哈希处理. 具体来说, 对于一个子段集合, 他的哈希值是$\sum base^{id(s_i)}$, 其中$s_i$是某一个子段的哈希值, $id(s_i)$表示离散化以后的值. $base$取大于$n$的数即可, 因为对于特定的$d$, 子串的总数量不会超过$n$.
平板电视yyds!其实是我不会写哈希表 :(
复杂度$O(\sum_{d=1}^{n} \frac{n}{d}) = O(nlogn)$
const int maxn = 3e5+10;
const int P = 998244353;
const int STR_BASE = 131;
const int M_BASE = 437977;
int t, n;
char s[maxn];
ULL str_base_pow[maxn], M_base_pow[maxn], pre_hash[maxn];
LL fac[maxn], inv[maxn];
__gnu_pbds::gp_hash_table <ULL, int> substr_cnt, row_id_map;
__gnu_pbds::gp_hash_table <ULL, bool> M_occur;
LL Mult(LL a, LL b) {
return a * b >= P ? a * b % P : a * b;
}
LL Plus(LL a, LL b) {
return a + b >= P ? (a + b) % P : a + b;
}
LL Power(LL a, LL b) {
LL res = 1;
while (b) {
if (b&1)
res = Mult(res, a);
a = Mult(a, a);
b >>= 1;
}
return res;
}
void Init() {
int N = 300000;
str_base_pow[0] = 1;
for (int i = 1; i <= N; i++)
str_base_pow[i] = str_base_pow[i-1] * STR_BASE;
M_base_pow[0] = 1;
for (int i = 1; i <= N; i++)
M_base_pow[i] = M_base_pow[i-1] * M_BASE;
fac[0] = inv[0] = 1;
for (int i = 1; i <= N; i++)
fac[i] = Mult(fac[i-1], i);
inv[N] = Power(fac[N], P-2);
for (int i = N - 1; i; i--)
inv[i] = Mult(i+1, inv[i+1]);
}
void InitStringPreHash() {
pre_hash[0] = 0;
for (int i = 1; i <= n; i++)
pre_hash[i] = pre_hash[i-1] * STR_BASE + s[i];
}
void Clear() {
substr_cnt.clear();
row_id_map.clear();
M_occur.clear();
}
int main() {
scanf("%d", &t);
Init();
for (int kase = 1; kase <= t; kase++) {
scanf("%s", s+1);
n = strlen(s+1);
InitStringPreHash();
LL ans = 0;
for (int d = 1; d <= n; d++) {
int N = n / d;
Clear();
int id_cnt = 0;
ULL M_hash = 0;
for (int i = 1; i <= N; i++) {
ULL hash_val = pre_hash[i*d] - str_base_pow[d] * pre_hash[(i-1)*d];
if (substr_cnt[hash_val])
substr_cnt[hash_val] += 1;
else
substr_cnt[hash_val] = 1;
int row_id;
if (row_id_map[hash_val])
row_id = row_id_map[hash_val];
else
row_id_map[hash_val] = row_id = ++id_cnt;
M_hash += M_base_pow[row_id];
}
LL res = fac[N];
for (auto p : substr_cnt)
res = Mult(res, inv[p.second]);
ans = Plus(ans, res);
int rem = n % d;
if (rem) {
M_occur[M_hash] = true;
for (int i = N; i; i--) {
ULL old_hash = pre_hash[i*d] - str_base_pow[d] * pre_hash[(i-1)*d];
int num = substr_cnt[old_hash];
res = Mult(res, fac[num]);
num--;
substr_cnt[old_hash] = num;
res = Mult(res, inv[num]);
ULL new_hash = pre_hash[i*d + rem] - str_base_pow[d] * pre_hash[(i-1)*d + rem];
if (substr_cnt[new_hash])
num = substr_cnt[new_hash];
else
num = 0;
res = Mult(res, fac[num]);
num++;
substr_cnt[new_hash] = num;
res = Mult(res, inv[num]);
int row_id;
if (row_id_map[new_hash])
row_id = row_id_map[new_hash];
else
row_id_map[new_hash] = row_id = ++id_cnt;
M_hash -= M_base_pow[row_id_map[old_hash]];
M_hash += M_base_pow[row_id];
if (!M_occur[M_hash]) {
ans = Plus(ans, res);
M_occur[M_hash] = true;
}
}
}
}
printf("Case #%d: %lld\n", kase, ans);
}
return 0;
}K. Kingdom’s Power
$T$组测试. $n$个点的有根树, 根为$1$, 初始根被占领, 且可以无限从根派兵去占领其他节点, 兵可以沿着边走(无向边, 可以返回来走), 每走一次花费为$1$. 问占领所有点最少需要多少花费.
$1 \le T \le 10^5, 1 \le n \le 10^6)$
据说有贪心, dp, 贪心+dp 的解法, 而且同一种方法的实现还不尽相同. 就很迷.
这道题我不会. 现在也没完全理解.
几个性质:
- 等价于占据所有叶子(证明略, 很简单)
- 存在树上的兵一定存在于叶子上(也很好证, 略)
张炀杰的做法:
先dfs一遍, 维护每个节点的深度和该子树的最大深度. 然后按照最大深度从小到大将儿子排序, 按这个顺序重新遍历, 依次记录叶子. 按这个顺序考虑占领每个叶子, 有这样一条神奇的性质:
- 如果当前叶子上的兵不去占领下一个叶子, 那么它不会去占领后面的叶子
感性理解一下是这样的…
证明? 不会呀!
然后就是模拟了, 需要用到lca, 倍增常数大, 考虑使用树剖(我写不动了…详细内容以后补吧, 咕咕咕)
复杂度$O(nlogn)$
const int maxn = 1e6+10;
int t, n, fa[maxn], dep[maxn], maxdep[maxn], top[maxn], size[maxn], bigson[maxn];
vector<int> son[maxn], leaves;
bool cmp(int u, int v) {
return maxdep[u] < maxdep[v];
}
void dfs1(int u, int d) {
dep[u] = maxdep[u] = d;
size[u] = 1;
for (auto v : son[u]) {
dfs1(v, d + 1);
maxdep[u] = max(maxdep[u], maxdep[v]);
size[u] += size[v];
if (size[v] > size[bigson[u]])
bigson[u] = v;
}
sort(son[u].begin(), son[u].end(), cmp);
}
void dfs2(int u, int tp) {
top[u] = tp;
for (auto v : son[u])
dfs2(v, v == bigson[u] ? tp : v);
if (!son[u].size())
leaves.pb(u);
}
int GetLca(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]])
swap(x, y);
x = fa[top[x]];
}
return dep[x] <= dep[y] ? x : y;
}
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d", &n);
leaves.clear();
for (int i = 1; i <= n; i++) {
son[i].clear();
bigson[i] = 0;
}
for (int i = 2; i <= n; i++) {
int f;
scanf("%d", &f);
fa[i] = f;
son[f].pb(i);
}
dfs1(1, 0);
dfs2(1, 1);
int last = 1, ans = 0;
for (auto u : leaves) {
ans += min(dep[u], dep[u] + dep[last] - 2 * dep[GetLca(u, last)]);
last = u;
}
printf("Case #%d: %d\n", kase, ans);
}
return 0;
}周灿的做法:
$O(n)$贪心好强呀, 我看不懂呀 %%% bzy %%%
$\color{red} {TUDO}$
周灿的代码(有空研究, 咕咕咕)
#include<bits/stdc++.h>
using namespace std;
int fa [1000005];
int deg[1000005];
int dep[1000005];
vector<int> V[1000005];
int main() {
int t; cin >> t;
for( int T = 1; T <= t; T ++ ) {
int n; cin >> n;
long long ans = 0;
for( int i = 1; i <= n; i ++ ) V[i].clear();
for( int i = 2; i <= n; i ++ ) scanf( "%d", fa + i ), deg[ fa[i] ] ++, dep[i] = dep[ fa[i] ] + 1;
queue<int> Q;
for( int i = 1; i <= n; i ++ ) if( !deg[i] ) Q.push(i), V[i].push_back(i), ans += dep[i];
while( Q.size() ) {
int x = Q.front(); Q.pop();
deg[ fa[x] ] --; if( !deg[ fa[x] ] ) Q.push( fa[x] );
int mx = 0;
for( auto c : V[x] ) if( dep[c] > dep[mx] ) mx = c;
for( auto c : V[x] ) if( mx ^ c ) if( dep[c] - dep[x] < dep[x] )
{ ans -= dep[x] - ( dep[c] - dep[x] ); }
V[ fa[x] ].push_back(mx);
}
printf( "Case #%d: ", T );
cout << ans << "\n";
}
}还有其他的dp做法, 我想的两个dp都写挂了…有空研究(咕咕咕)
UPD(2020-10-28): 没咕!
设$dp_1(u)$为 点$u$有一个并, 只用这一个兵走完以$u$为根的子树, 并且回到$u$需要的步数; $dp_2(u)$为 从根节点$(1)$出若干个兵, 走完$u$这棵子树, 并且兵停在某些叶子需要的最小步数.
答案很显然是$dp_2(1)$
下面想转移:
很容易转移$dp_1(u)$,
$$dp_1(u) = \sum_{v \in SON_u} (dp_1(v) + 2)$$
很显然, 这个兵往下走需要一次, 走完后回来需要一次, 所以一条边加两次.
如何转移$dp_2$呢??
首先有一个树形$dp$的常用性质:
如果对一个节点$u$, 当前已经考虑完了若干个儿子, 并且完成了儿子到$u$的转移, 即得到了"部分"的$dp(u)$. 这时的$dp(u)$是有意义的, 即"$u$和已经做完的儿子构成的子树(为方便, 称它为’当前子树’)的$dp$值", 如图:
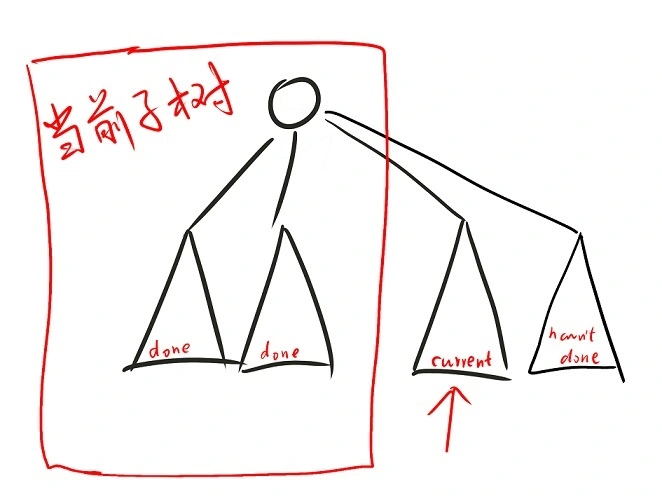
这样就可以合理利用"已经做完的所有儿子", 而不是枚举做完的儿子. 当然前提是状态要定义得好.
回到本题, 考虑当前儿子$v$, 可能有三种情况:
-
做完的儿子中的某一个兵回到$u$, 它再走$v$. 注意这样的话可以用他来"替换"一个$dp_2(x) \mid x \in Tree_v$的花费(停在$Tree_v$的其他兵的花费是直接算的$dp_2$, 从根下来的, 不与当前做法冲突)
-
$v$做完后, 一个兵回到$u$, 去走"做完"的儿子(利用"当前子树", 即可考虑所有"做完"的儿子[为什么打引号呢? 因为这一步改变了"当前子树"的策略, 也就是说, 当前子树的当前策略并不是最终策略])
-
直接从根新派若干个兵走完$v$
对应的三个花费分别是:
$$ \begin{aligned} & dp_1(u) + dp_2(v) \\ & dp_2(u) + dp_1(v) + 2 \\ & dp_2(u) + dp_2(v) \end{aligned} $$
前两个看着很迷?
解读一下, 以第一个决策的花费为例:
$dp_2(v)$被分为了两个部分, $1 — u — Tree_v$; 而$dp_1(u)$只是$CurrentTree_u — back\ to\ u$一个部分, 重新组合一下, 变成$1 — CurrentTree_u — back\ to\ u — Tree_v$, 这样就是实际上的路线了
第二个也是同理拆分重组
结合上述分析和方程, 再理解一下决策…
…
可以发现, 决策1和2恰好是"对称"的, 考虑了全部的"兵回到$u$再走其他儿子"的情况; 同时有第三个决策, 考虑了从根下来的情况, 弥补了前两个方程"只是一个兵在走"的不足. 所以, 这种转移考虑到了所有的情况, 是合理且巧妙的.
那么新的当前子树$dp_2$的值就对上述三种决策的花费最小即可.
最后确定边界条件. 树形dp的边界是叶子, 但是这里有一个不是常规的树形dp定义法, $dp_2$居然和根扯上了关系. 可以理解为, 结点本身就有一个花费(从根走到该节点的步数, 即深度), 把他加在$dp_2$上即可. $dp_1$的初始值为$0$.
独立思考我绝对想不到这样的做法, 太妙了, 下次补"为什么这么想"吧, 咕咕咕
复杂度$O(n)$
const int maxn = 1e6+10;
int t, n, ans, dp1[maxn], dp2[maxn];
vector<int> son[maxn];
void dfs(int u, int d) {
dp1[u] = 0;
dp2[u] = d;
for (auto v : son[u]) {
dfs(v, d + 1);
dp2[u] = min(min(dp1[u] + dp2[v], dp2[u] + dp1[v] + 2), dp2[u] + dp2[v]);
dp1[u] += dp1[v] + 2;
}
}
int main() {
scanf("%d", &t);
for (int kase = 1; kase <= t; kase++) {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
son[i].clear();
for (int i = 2; i <= n; i++) {
int f;
scanf("%d", &f);
son[f].pb(i);
}
dfs(1, 0);
printf("Case #%d: %d\n", kase, dp2[1]);
}
return 0;
}