2020-2021 ACM-ICPC Brazil Subregional Programming Contest M. Machine Gun
在二维平面上给出 $n$ 个敌军的坐标 $A_i(x_i, y_i)$, 再进行q次强制在线询问:
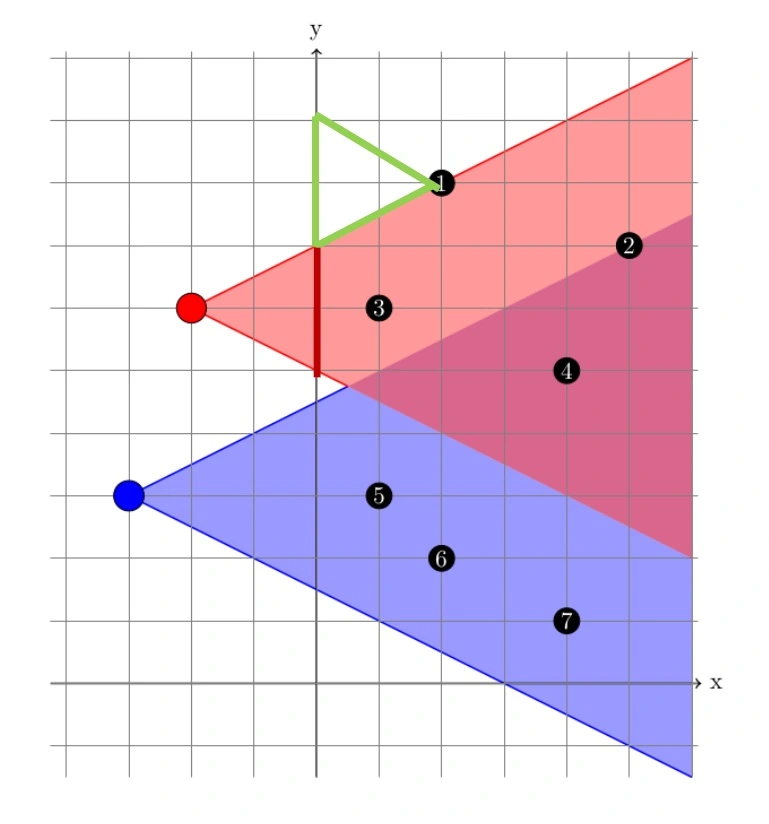
每次询问将给出一个炮台坐标 $(x_m, y_m)$, 需找出所有能被坐标 $(x_m, y_m)$ 攻击到的敌军的下标. 这里定义炮台 $(x_m, y_m)$ 能攻击到的范围是 $y = y_m \pm \frac{x - x_m}{2}$ 所夹出来的右半部分, 包括边界.
接下来将这些下标按照升序排序, 记为$i_0, i_1, \dots i_k$
计算结果 $(\sum_{j=0}^{k-1} i_j \cdot 5782344^j) \mod 10^9 + 7$, 输出结果.
$1 \le x_i, y_i \le 10^9, 1 \le n, q, \le 10^5$
保证所有查询中被攻击到的敌军总数不超过 $10^6$, 保证$x_i > 0, x_m < 0$
有两种考虑方式.
第一种
施鹏飞学长讲的:
注意到每个炮台所能攻击到的范围角度是固定的, 所以为了更好地刻画炮台 攻击的覆盖范围, 我们可以将炮台的攻击范围投影到$x=0$这条线上; 类似地, 将每个敌军以同样的角度都投影到$x=0$这条线上. 如果两条线段有交集, 那么 该炮台就可以攻击到这个敌军.
线段
问题就等价地转化为: 在数轴上给出 $n$ 个区间, 再进行 $q$ 次 查询, 每次查询给出一个区间, 询问 $n$ 个区间中有哪些区间与询问的区间相交.
形式化一下, 我们要找这样的区间: $l_i \le r_m, r_i \ge l_m$, 其中 $[l_m, r_m]$是询问区间.
第二种
将坐标进行伸缩变换:
- 把两条边的夹角改成直角: $y \to 2y$
- 把 $x$ 轴 $y$ 轴顺时针转 $\frac{\pi}{4}$: $(x, y) \to (x - y, x + y)$
总的来说, 把 $(x, y) \to (x - 2y, x + 2y)$.
也就是说, 令每个点的坐标为 $\begin{cases} x’ = x - 2y \\ y’ = x + 2y \end{cases}$
也就是得到下面这种东西:
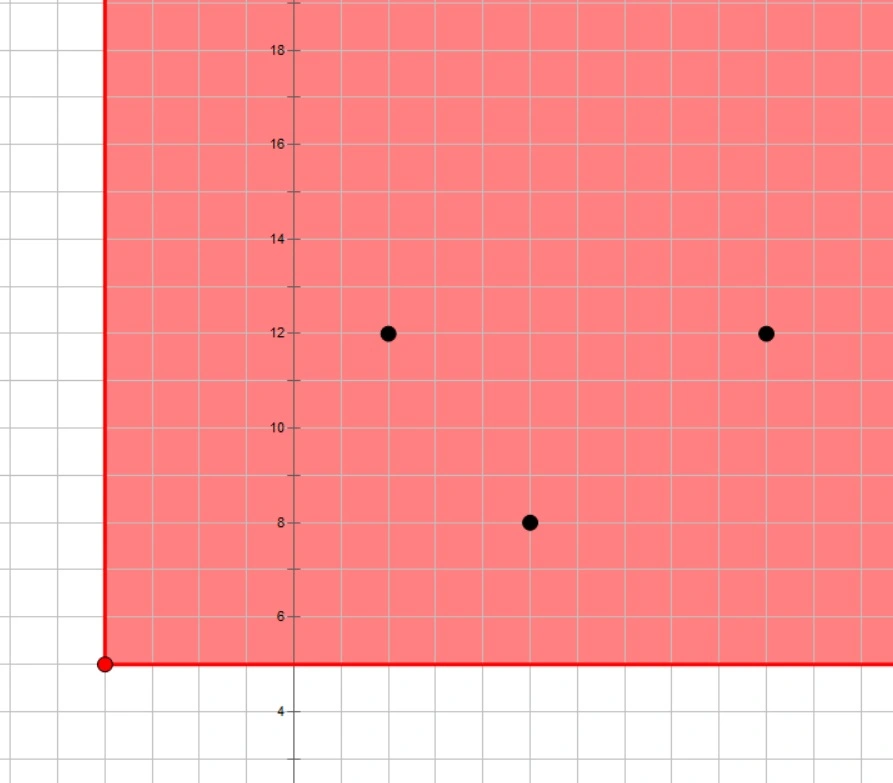
然后找这样的点: $x_i’ \ge x_m’, y_i’ \ge y_m'$
实际上两者没有本质区别, 最后得到的关系都是一样的, 只是思考方式的不同.
当然还有第三种方法, 就是直接推算满足什么样的条件的点会被炮塔打到. 得到的结果是一样的.
到这里就转换成了二维偏序问题. 先对一维排序, 然后再放到数据结构上排第二维.
这里需要的不是个数, 而是所有的点的下标. 所以考虑用线段树, 每个节点开一个 vector 按第二维的顺序存 第二维和原下标(需要第二维排序, 需要原下标).
二分确定第一维的范围, 在线段树上区间查询第二维即可. 二维偏序就是这个套路.
复杂度 $O(n \log n + q \log^2 n)$
const int P = 1e9 + 7;
const LL BASE = 5782344;
const int MAXN = 1e5+10;
int Plus(LL a, LL b) {
return a + b >= P ? (a + b) % P : a + b;
}
int Mult(LL a, LL b) {
return a * b >= P ? a * b % P : a * b;
}
struct Seg {
LL l, r, id;
bool operator < (const Seg &S) const {
return r == S.r ? l == S.l ? id < S.id : l < S.l : r < S.r;
}
} segs[MAXN];
int n, q;
LL p = 0;
Seg calc_seg(LL x, LL y, int id) {
LL l = 2 * y - x, r = 2 * y + x;
if (l > r)
swap(l, r);
return Seg{l, r, id};
}
struct SegTree {
struct Node {
int l, r, mid;
vector<PLI> v;
};
vector<Node> tree;
SegTree(int _n, Seg data[]) {
tree.resize(_n << 2);
build(data, 1, _n);
}
void push_up(int u) {
vector<PLI> &lv = tree[LCH(u)].v, &rv = tree[RCH(u)].v, &v = tree[u].v;
int i = 0, j = 0, len_l = lv.size(), len_r = rv.size();
while (i < len_l && j < len_r) {
if (lv[i] < rv[j])
v.push_back(lv[i++]);
else
v.push_back(rv[j++]);
}
while (i < len_l)
v.push_back(lv[i++]);
while (j < len_r)
v.push_back(rv[j++]);
}
void build(Seg data[], int l, int r, int u = 1) {
tree[u] = Node{l, r, (l + r) >> 1};
tree[u].v.clear();
if (l == r)
tree[u].v.push_back(make_pair(data[l].l, data[l].id));
else {
build(data, l, tree[u].mid, LCH(u));
build(data, tree[u].mid + 1, r, RCH(u));
push_up(u);
}
}
void add_ans(set<LL> &res, LL r, int u) {
for (auto x : tree[u].v) {
if (x.first > r)
break;
else
res.insert(x.second);
}
}
void query(set<LL> &res, LL rr, int l, int r, int u = 1) {
if (l == tree[u].l && r == tree[u].r)
add_ans(res, rr, u);
else {
if (l > tree[u].mid)
query(res, rr, l, r, RCH(u));
else if (r <= tree[u].mid)
query(res, rr, l, r, LCH(u));
else {
query(res, rr, l, tree[u].mid, LCH(u));
query(res, rr, tree[u].mid + 1, r, RCH(u));
}
}
}
};
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++) {
LL x, y;
scanf("%lld%lld", &x, &y);
segs[i] = calc_seg(x, y, i);
}
sort(segs + 1, segs + 1 + n);
SegTree T(n, segs);
while (q--) {
LL a, b;
scanf("%lld%lld", &a, &b);
LL x = - 1 - Plus(p, a), y = Plus(p, b);
Seg s = calc_seg(x, y, 0);
int pos = lower_bound(segs + 1, segs + 1 + n, Seg{-INF, s.l, 0}) - segs;
p = 0;
if (pos <= n) {
set<LL> res;
res.clear();
T.query(res, s.r, pos, n);
LL power = 1;
for (auto x : res) {
p = Plus(p, Mult(power, x));
power = Mult(power, BASE);
}
}
printf("%lld\n", p);
}
return 0;
}