点分治
感谢 LittleChai 教会了我点分治!
板题引入
点分治用来处理许多(一般是所有)树上点对信息, 比如路径.
比如洛谷上的板题:
给定一棵有 $n$ 个点的树, $m$ 次询问, 问树上距离为 $k$ 的点对是否存在.
暴力是枚举两个点 $x, y$, 然后求 $lca$, 再算 $dist(lca, x) + dist(lca, y)$
现在我们这么思考: 对于一棵树, 我们把路径(点对)分成两种:
- 经过根的
- 不经过根的
此时, 经过根的路径就类似于lca那样, 可以被分为两段: $dist(x, root)$ 和 $dist(y, root)$. 假设我们处理出了所有的 $dist(v, root)$(其中 $v$ 为 $root$ 的后代), 那么枚举一下所有的 $dist(u, root)$, 就变成了判断是否存在 $dist(v, root) = k - dist(u, root)$. 当然这里会出现这样的情况, 需要容斥一下, 待会再详细讲:
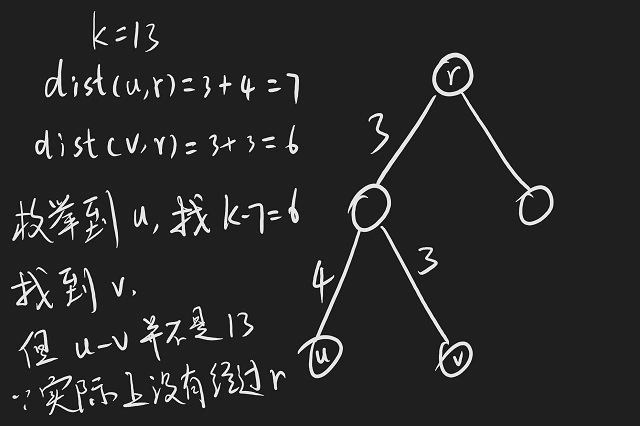
然后我们考虑不经过根的路径.
这时, 所有经过根的路径已经被处理完了, 所以根这个点可以删掉了.
于是, 剩下了一些子树. 在这些子树中, 我们又可以用同样的方法考虑点对.
由于求点对信息(路径等)的话, 根的选取不改变树的结构, 所以这个"根"我们是可以随便选的. 如何选最优呢? 答案是选重心. 重心能把子树的高度尽可能划分成最小, 这样在继续分治的过程中就可以减小操作的次数了. 可以证明, 这样的操作考虑所有点的复杂度是 $O(nlogn)$的(口胡).
接下来, 我们考虑容斥掉多算了的.
还是上面那个例子, $s$ 是 $r$ 的儿子, $u, v$点对是"非法的", 因为他的路径其实不经过 $r$. 所以我们要去掉这个. 这一条"路径"(这里的路径也是假的, 下面有解释)一定会经过 $s$, 所以我们在子树 $s$ 中, 减去长度为 $k - 2w(r, s)$的路径即可. 在实现的过程中是这样做的: 把 $k$ 看成 $dist_1 + dist_2$, 然后把两个距离都"加上" $w$, 这样目标长度还是 $k$, 做到了统一.
这种情况呢? 解释在图里, 并且也说明了路径为什么打引号.

至此, 我们就大概做完了这题.
当然不是所有的题都要容斥掉一部分, 具体题目还得具体分析. 如果点对信息是路径的话, 由于重心并不是lca, 所以会"多算了".
更多板题
再来看一道板题聪聪可可:
求树上点对路径为 $3$ 的倍数的有多少条(有序对)
还是一样, 先找重心, 然后求子代到重心的路径长度. 由于只计算$3$的倍数, 所以长度对 $3$ 取模, 路径条数存在大小为 $3$ 的桶里. 设长度模 $3$ 为 $i$ 的子代到重心的路径为 $t_i$, 那么经过重心的路径长度为$3$的倍数的条数有 $t_0^2 + 2t_1t_2$. 当然此时有"不合法路径", 由于"不合法路径"经过重心的儿子, 所以求儿子的子代到儿子的路径长度, 一样丢在桶里, $t_0’ + 2t_1’t_2’$ 就是不合法的路径条数, 减去就是真正的所有经过重心的长度为 $3$ 的倍数的路径了.
然后我们处理经过其他点的路径. 再从子树中找重心, 重复上述过程即可.
再来看一道板题(LittleChai讲的, 我还没去找题目链接):
求树上点对路径大于 $k$ 的有多少条.
还是一样的做法, 先把每一个 $dist(v, c)$ 求出来, 然后丢到权值BIT中. 之后再遍历每一个 $dist$, 求出大于 $k - dist$ 的有多少. 注意不要求到自己. 可以先在BIT中减去当前枚举的 $dist$, 求完以后再插回去. 同理需要容斥.
高级处理
最后再来仔细分析一下去年vp的韩国一场open cup的一个点分治
分析个屁不会做, 看题解+思考好久才能明白, 也说不清楚, 考场也想不到, 我是废物!
以后能力强了再来看看能不能解释明白吧. 等那一天解释明白了考场才能想到这样的做法吧.
模板代码
int sz[MAXN], vis[MAXN]; // sz[u] 为每次dfs计算以u为根的子树的大小
// descendant 保存第一次调用dfs的点u到包含u的树中的所有的点v及他们之间的距离
vector<PII> descendant;
/* 遍历, 同时计算sz和descentant */
/* dis是根(第一次调用dfs的点)到当前点u的距离(如果第一次调用dis参数为0, 不为0的话会在所有距离上加上这个参数) */
void dfs(int u, int f, int dis) {
sz[u] = 1;
descendant.emplace_back(u, dis);
for (int i = head[u]; i; i = edges[i].next) {
Edge &e = edges[i];
if (e.to != f && !vis[e.to]) {
dfs(e.to, u, dis + e.w);
sz[u] += sz[e.to];
}
}
}
/* 求包含u的树的重心 */
int center(int u) {
// 每一次求重心的时候, 要重新求子代, 注意清空
descendant.clear();
dfs(u, 0, 0);
int tot_sz = descendant.size();
for (auto des : descendant) {
int is_center = 1;
int x = des.first;
for (int i = head[x]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to])
continue;
// sz[x] > sz[v] == v 是 x 的儿子
// sz[v] > n / 2, v 不是重心
if (sz[x] > sz[e.to] && (sz[e.to] << 1) > tot_sz) {
is_center = 0;
break;
}
// sz[x] < sz[v] == v 是 x 的父亲
// tot_sz - sz[x] 是 v "向上"的子树大小
// tot_sz - sz[x] > n / 2, v 不是重心
if (sz[x] < sz[e.to] && ((tot_sz - sz[x]) << 1) > tot_sz) {
is_center = 0;
break;
}
}
if (is_center) {
// 找到重心, 需要以重心为根, 求一下树中所有点到重心的距离
// 这样调用完center后就可以保存所有点到重心的距离了
descendant.clear();
dfs(x, 0, 0);
return x;
}
}
return -1;
}
void divide(int u) {
int c = center(u);
vis[c] = 1; // 标记重心, 删去
work(); // 已经在center函数中处理了 "经过重心的'半路径'", 在work函数中考虑如何把两条半路径组合成一条路径, 并考虑如何处理数据, 回答问题
for (int i = head[c]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to]) // v 已经删除, 不考虑
continue;
iework(); // 考虑把"假的路径"容斥掉. 如果是路径, 那么求一次dfs(e.to, c, e.w)得到的descentant就是所有"假的路径". 这时候虽然第一次调用dfs的是e.to, 但由于加上的e.w, 也可以认为是点到c的距离
divide(e.to); // 找到剩余的点(所在的子树), 继续处理
}
}板题代码
洛谷模板题点分治1
这题要注意不能处理出所有"半路径"以后枚举两条拼凑, 这样复杂度是 $O(n^2)$ 的. 注意到询问只有 $100$ 个, 所以可以枚举询问和一条半路径, 判断能够凑成询问的另一半是否存在. 这样复杂度是 $O(mn)$
总复杂度 $O(mnlogn)$
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <stack>
#define lowbit(x) (x&(-x))
#define LCH(x) (x<<1)
#define RCH(x) (x<<1|1)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef long double LD;
typedef pair<int, int> PII;
typedef vector<int> VI;
const int INTINF = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e4+10;
const int MAXK = 1e7+10;
const int MAXM = 110;
struct Edge {
int to, next, w;
} edges[MAXN<<1];
int mm = 0, head[MAXN];
void addEdge(int u, int v, int w) {
edges[++mm] = Edge{v, head[u], w};
head[u] = mm;
}
void addNet(int u, int v, int w) {
addEdge(u, v, w);
addEdge(v, u, w);
}
int n, q, k[MAXM], t[MAXK], sz[MAXN], vis[MAXN], ans[MAXM];
vector<PII> descendant;
void dfs(int u, int f, int dis) {
sz[u] = 1;
descendant.emplace_back(u, dis);
for (int i = head[u]; i; i = edges[i].next) {
Edge &e = edges[i];
if (e.to != f && !vis[e.to]) {
dfs(e.to, u, dis + e.w);
sz[u] += sz[e.to];
}
}
}
int center(int u) {
descendant.clear();
dfs(u, 0, 0);
int tot_sz = descendant.size();
for (auto des : descendant) {
int is_center = 1;
int x = des.first;
for (int i = head[x]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to])
continue;
if (sz[x] > sz[e.to] && (sz[e.to] << 1) > tot_sz) {
is_center = 0;
break;
}
if (sz[x] < sz[e.to] && ((tot_sz - sz[x]) << 1) > tot_sz) {
is_center = 0;
break;
}
}
if (is_center) {
descendant.clear();
dfs(x, 0, 0);
return x;
}
}
return -1;
}
void divide(int u) {
int c = center(u);
vis[c] = 1;
for (auto des : descendant) if (des.second <= 1e7)
t[des.second]++;
for (int i = 1; i <= q; i++)
for (auto des : descendant) {
if (k[i] - des.second >= 0)
ans[i] += t[k[i] - des.second] > 0;
}
for (auto des : descendant) if (des.second <= 1e7)
t[des.second]--;
for (int i = head[c]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to])
continue;
descendant.clear();
dfs(e.to, c, e.w);
for (auto des : descendant) if (des.second <= 1e7)
t[des.second]++;
for (int i = 1; i <= q; i++)
for (auto des : descendant)
if (k[i] - des.second >= 0)
ans[i] -= t[k[i] - des.second] > 0;
for (auto des : descendant) if (des.second <= 1e7)
t[des.second]--;
divide(e.to);
}
}
int read() {
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*f;
}
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i < n; i++) {
int u = read(), v = read(), w = read();
addNet(u, v, w);
}
for (int i = 1; i <= q; i++)
scanf("%d", k + i);
divide(1);
for (int i = 1; i <= q; i++)
puts(ans[i] ? "AYE" : "NAY");
return 0;
}#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <stack>
#define lowbit(x) (x&(-x))
#define LCH(x) (x<<1)
#define RCH(x) (x<<1|1)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef long double LD;
typedef pair<int, int> PII;
typedef vector<int> VI;
const int INTINF = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 2e4+10;
struct Edge {
int to, next, w;
} edges[MAXN<<1];
int mm = 0, head[MAXN];
void addEdge(int u, int v, int w) {
edges[++mm] = Edge{v, head[u], w};
head[u] = mm;
}
void addNet(int u, int v, int w) {
addEdge(u, v, w);
addEdge(v, u, w);
}
int n, t[5], sz[MAXN], vis[MAXN], ans = 0;
vector<PII> descendant;
void dfs(int u, int f, int dis) {
sz[u] = 1;
descendant.emplace_back(u, dis%3);
t[dis%3]++;
for (int i = head[u]; i; i = edges[i].next) {
Edge &e = edges[i];
if (e.to != f && !vis[e.to]) {
dfs(e.to, u, (dis + e.w)%3);
sz[u] += sz[e.to];
}
}
}
int center(int u) {
descendant.clear();
t[0] = t[1] = t[2] = 0;
dfs(u, 0, 0);
int tot_sz = descendant.size();
for (auto des : descendant) {
int is_center = 1;
int x = des.first;
for (int i = head[x]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to])
continue;
if (sz[x] > sz[e.to] && (sz[e.to] << 1) > tot_sz) {
is_center = 0;
break;
}
if (sz[x] < sz[e.to] && ((tot_sz - sz[x]) << 1) > tot_sz) {
is_center = 0;
break;
}
}
if (is_center) {
descendant.clear();
t[0] = t[1] = t[2] = 0;
dfs(x, 0, 0);
return x;
}
}
return -1;
}
void divide(int u) {
int c = center(u);
vis[c] = 1;
ans += t[0] * t[0] + 2 * t[1] * t[2];
for (int i = head[c]; i; i = edges[i].next) {
Edge &e = edges[i];
if (vis[e.to])
continue;
descendant.clear();
t[0] = t[1] = t[2] = 0;
dfs(e.to, c, e.w);
ans -= t[0] * t[0] + 2 * t[1] * t[2];
divide(e.to);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
addNet(u, v, w);
}
divide(1);
int d = __gcd(ans, n * n);
printf("%d/%d\n", ans/d, n*n/d);
return 0;
}