一个 $n \times n$ 的棋盘上会有 $m$ 次变化, 每次变化都会在某个空的位置上出现一个兵 或者 移去存在棋盘上的某个兵. 一个兵处于坐标 $(x, y)$ 可以移动到 $(x, y + 1)$, $(x − 1, y + 1)$ 或 $(x + 1, y + 1)$, 前面是列, 后面是行. 有一个特殊列 $k$, 每次变化, 你都要计算把所有的兵移动到第 $k$ 列(不可以重叠), 需要在棋盘上第 $n$ 之后额外添加的最少行数.
$1 \le n, m \le 2 \cdot 10^5, 1 \le k \le n$
首先把棋子都用最近的移动方式移动到第 $k$ 列, 可让他们重叠在一格里. 这样就变成一维的问题了.
考虑这个一维的序列, 如图, 我们需要把多的兵往下移.
把多的兵往下移动
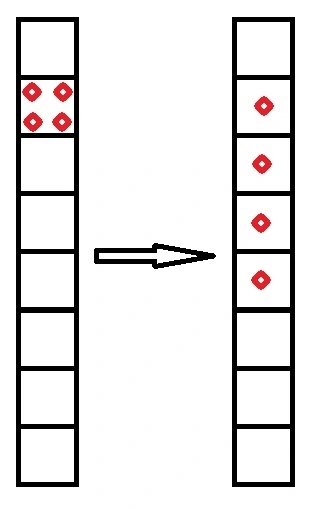
我们记录这个点的权值为当把所有兵依次往下放, 走的最远的那个兵的行号. 图中即 $w(2) = 5$.
要维护这样的一个权值, 首先可以考虑初始化第 $i$ 行的权值为 $i-1$, 然后这一个点出现一个兵, 就把这个点的权值 $+1$; 同理消失一个兵就 $-1$.
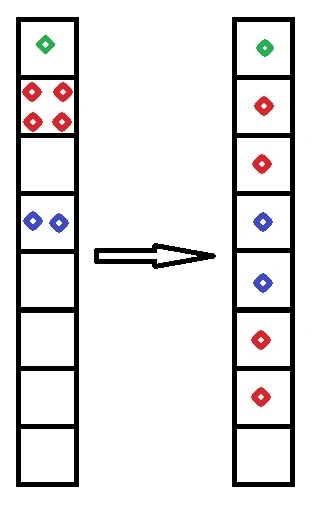
但是会出现这样的情况: 上面要走的兵与下面有的兵冲突了! 见下图左.
冲突了
我们先让下面蓝色的兵走, 然后再让上面红色的兵"跳过"蓝色的兵, 走到蓝色底下, 见上图右.
这样就有 $w(2) = 6, w(4) = 7$.
按照这样的想法, 下面的兵会对上面的兵产生影响, 而影响就是让上面的权值增加. 增加的数量就是下面的兵的数量.
那么我们可以用线段树维护一段 $2n$ 的序列: 先初始化每个点为$i-1$, 在 $pos$ 位置放一个兵, 就让区间 $[1, pos]$ 都 $+1$; 拿走就 $-1$. 然后取区间 $[1, pos_{last}]$ 中的最大值, 就是最远放的兵了.
注意, 这个线段树中不是每个点的权值都有"实际意义". 比如, 没有兵的点, 权值不能代表什么. 有兵的点, 权值可能大于"这个点的所有兵能走的最远行号", 比如这样:
不是所有的点都有意义
我们认为的$w(1) = 1$, 而按照上述维护线段树的方法, 得到在 $1$ 处的值是 $7$.
这种情况其实不用担心, 因为最远的那个兵对应的起点, 在线段树上的值就是$w$, 而取max一定是取到最远的兵.
出现位置用 set 记录一下就就行.
复杂度$O(mlogn + mlogm)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
|
const int MAXN = 2e5+10;
int n, k, q;
struct SegTree {
struct Node {
int l, r, mid, val, tag;
};
int n;
vector<Node> tree;
void init(int _n) {
n = _n;
tree.clear();
tree.resize((n+10) << 2);
}
void push_up(int u) {
tree[u].val = max(tree[LCH(u)].val, tree[RCH(u)].val);
}
void build(int u, int l, int r, VI &data) {
tree[u] = Node{l, r, (l + r) >> 1, 0, 0};
if (l == r)
tree[u].val = data[l];
else {
build(LCH(u), l, tree[u].mid, data);
build(RCH(u), tree[u].mid + 1, r, data);
push_up(u);
}
}
void build(VI &data) {
build(1, 1, n, data);
}
void update_node(int u, int d) {
tree[u].val += d;
tree[u].tag += d;
}
void push_down(int u) {
update_node(LCH(u), tree[u].tag);
update_node(RCH(u), tree[u].tag);
tree[u].tag = 0;
}
void update(int l, int r, int d, int u = 1) {
if (tree[u].l == l && tree[u].r == r)
update_node(u, d);
else {
push_down(u);
if (r <= tree[u].mid)
update(l, r, d, LCH(u));
else if (l > tree[u].mid)
update(l, r, d, RCH(u));
else {
update(l, tree[u].mid, d, LCH(u));
update(tree[u].mid + 1, r, d, RCH(u));
}
push_up(u);
}
}
int query(int l, int r, int u = 1) {
if (tree[u].l == l && tree[u].r == r)
return tree[u].val;
else {
push_down(u);
if (r <= tree[u].mid)
return query(l, r, LCH(u));
else if (l > tree[u].mid)
return query(l, r, RCH(u));
else
return max(query(l, tree[u].mid, LCH(u)), query(tree[u].mid + 1, r, RCH(u)));
}
}
};
int main() {
#ifdef GDB
freopen("B.in", "r", stdin);
// freopen("B.out", "w", stdout);
#endif
scanf("%d%d%d", &n, &k, &q);
SegTree tree;
tree.init(n<<1);
VI data = {0};
for (int i = 1; i <= n<<1; i++)
data.push_back(i-1);
tree.build(data);
set<PII> apd;
multiset<int> ocp;
while (q--) {
int x, y;
scanf("%d%d", &x, &y);
PII cood = {x, y};
int pos = y + abs(x - k);
if (apd.find(cood) != apd.end()) {
apd.erase(cood);
ocp.erase(ocp.find(pos));
tree.update(1, pos, -1);
}
else {
apd.insert(cood);
ocp.insert(pos);
tree.update(1, pos, 1);
}
if (ocp.empty())
puts("0");
else
printf("%d\n", max(0, tree.query(1, *ocp.rbegin()) - n));
}
return 0;
}
|