给出两个字符串$s_0, t$, 其中$|s_0| \le 100, |t| \le n$. 设$s_{i+1} = s_i + t_i + s_i$, + 表示字符串连接. $q$ 个询问, 形如 k sq, $k$是整数, $sq$ 是非空字符串, 表示询问 $s_k$ 中, $sq$ 的出现次数.
$k < n \le 10^5, q \le 10^6$
首先注意到, $sk$ 的长度是指数爆炸的, 所以不能完全构造出来.
但是 $sq$ 比较短, 我们可以构造出长度恰好大于等于 $sq$ 的$skk$. 注意到 $|skk| \le 2|sq| + 1$这样的话可以在 $O(2|sq|)$ 内求出 $sq$ 在 $skk$ 中出现了几次. KMP或者hash都能做.
$s_{kk+1} = skk + tkk + skk$, 会发现, $skk$已经算过了, 要计算的就是**包含$tkk$**的字符串中, $sq$ 出现的次数.
我们可以这样构造:
先取出$skk$的长度等于$|sq|-1$的后缀$suf$, 再取出长度等于$|sq|-1$的前缀$pre$, 构造$st = suf + tkk + pre$, 这样求 $sq$ 在 $st$ 中出现的次数, 就是包含 $tkk$ 的次数了.
根据上述推导, 我们能够整出一个递推式: 设$f(i)$为 $sq$ 在 $s_i$ 中出现的次数, 有
$$f(i) = 2f(i-1) + (sq \text{在当前} st \text{中出现的次数})$$
设 $g(i) = (sq \text{在算f(i)的} st \text{中出现的次数})$, 对应上式的 $st$ 那一部分的贡献.
这个递推式很简单, 类似二进制, 我们可以直接写出 $f(k)$ 的表达式
$$f(k) = 2^{k-kk}f(kk) + \sum_{i=kk+1}^k 2^{k-i}g(i)$$
我们已经算过 $f(kk)$ 了, 现在要求的是后面一个式子.
可以发现, 当$|skk| \ge |sq|$ 时, 在$t_i, i>kk$旁边的永远都是$suf$和$pre$. 证明简单, 可参考官方题解.
所以, 我们可以预处理一下 $skk + T + skk$, 其中 $T$ 取遍字符集, 即 $26$ 个小写字母. 当 $t_i = c$ 时, 我们就加上 $2^{k-i} \cdot (sq \text{在} skk + c + skk \text{中出现次数})$.
那么, 可以这样转化贡献:
我们遍历这$26$个字母, 当$t_i = c$时加上上述贡献, $t_i \ne c$时不加贡献. 结合下图理解一下:
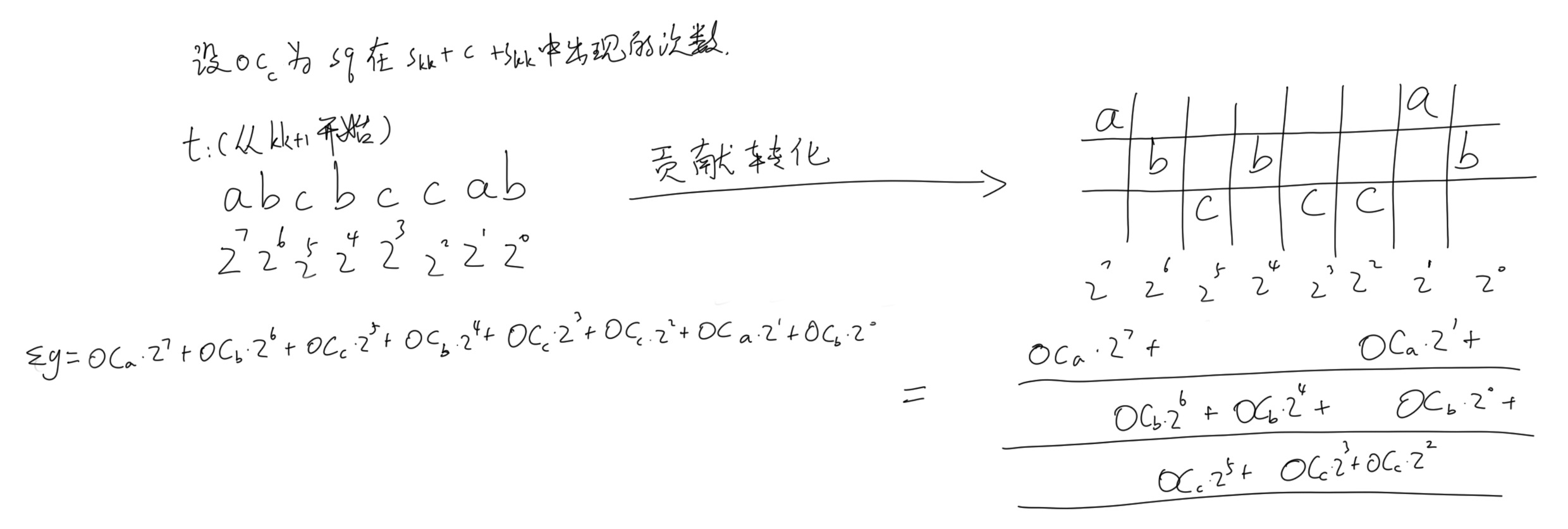贡献转化示意图
由于 $t_i$ 取相同值是, $oc_c$ 是相同的, 所以我们甚至可以把他提出来, 那么剩下的部分就是一堆二的次幂的和, 这些和就可以看作 $oc_c$ 的贡献.
我们可以预处理出这些和, 那么就可以从遍历$26$个字母, 求 $oc_{c} \cdot \text{贡献}$ 加入答案.
这一部分的共贡献可以用类似哈希(或者说p进制)的做法求, 只不过要对每一个字符都做一遍, 得到 $26$ 个 sum[i], 然后分别对应地算 $sum[k] - sum[kk]$就是这些贡献了. 乘到$oc_{c}$上就是对答案的贡献.
于是每一次询问就可以在$O(26)$内算出答案了.
还要注意可能 $|sq| > |sk|$, 这样我们的算法做出来会有 $kk > k$, 特判一下这种情况答案是$0$.
有点绕, 写完还是没有特别清楚这个转化过程, 还需要多看多想.
总复杂度$O(q)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
const int P = 1e9 + 7;
const int MAXN = 1e5+10;
const int MAXM = 1e6+10;
int Plus(LL a, LL b) {
return a + b >= P ? (a + b) % P : a + b;
}
int Minus(LL a, LL b) {
return Plus(a, P-b);
}
int Mult(LL a, LL b) {
return a * b >= P ? a * b % P : a * b;
}
int n, q, k, ans = 0, oc[30];
char s0[110], t[MAXN], sq[MAXM];
string get_sw(int len, int &cur, int &cur_len) {
cur_len = strlen(s0);
string s_cur = s0;
while (cur_len < len) {
s_cur = s_cur + t[cur++] + s_cur;
cur_len = cur_len * 2 + 1;
}
return s_cur;
}
int f[MAXM];
void kmp_init(int len) {
f[0] = f[1] = 0;
int j = 0;
for (int i = 1; i < len; i++) {
j = f[i];
while (j && sq[i] != sq[j])
j = f[j];
f[i+1] = sq[i] == sq[j] ? j+1 : 0;
}
}
int kmp(string T, int len2) {
int cnt = 0, j = 0, len1 = T.length();
for (int i = 0; i < len1; i++) {
while (j && T[i] != sq[j])
j = f[j];
if (T[i] == sq[j])
j++;
if (j == len2)
cnt++;
}
return cnt;
}
int pw[MAXN], sum[30][MAXN];
void init() {
pw[0] = 1;
for (int i = 1; i <= n; i++)
pw[i] = Mult(pw[i-1], 2);
for (char c = 'a'; c <= 'z'; c++) {
for (int i = 0; i < n; i++)
sum[c-'a'][i+1] = Plus(Mult(sum[c-'a'][i], 2), t[i] == c);
}
}
int main() {
scanf("%d%d%s%s", &n, &q, s0, t);
init();
while (q--) {
scanf("%d%s", &k, sq);
int sq_len = strlen(sq);
kmp_init(sq_len);
int kk = 0, sw_len = 0;
string sw = get_sw(sq_len, kk, sw_len);
int occ = kmp(sw, sq_len);
if (k >= kk) {
ans = Mult(occ, pw[k-kk]);
for (char c = 'a'; c <= 'z'; c++) {
string st = sw.substr(sw_len - sq_len + 1, sq_len-1) + c + sw.substr(0, sq_len-1);
oc[c-'a'] = kmp(st, sq_len);
ans = Plus(ans, Mult(oc[c-'a'], Minus(sum[c-'a'][k], Mult(sum[c-'a'][kk], pw[k-kk]))));
}
}
else
ans = 0;
printf("%d\n", ans);
}
return 0;
}
|