深入理解期望DP
打牛客发现完全不会概率期望, 高中课本上的东西就是个屑, 大概率徐积限自己也不清楚就乱教. 冥思苦想, 用自己的方式理解了一波, 记录一下.
随机事件
随机事件是一个事件, 他每次发生的结果是随机的, 并不能确定. 比如投掷骰子, 向上的点数就是一个随机事件. 如果投掷一次, 骰子向上的点数为 $3$, 下一次投掷, 向上的点数也不一定是 $3$, 发生哪个事件, 即向上的点数是多少, 完全随机, 无法确定.
随机变量
本文仅讨论离散随机变量, 后文的随机变量均指离散随机变量.
传统意义上的变量只可能有一个取值, 只不过我们不知道而已. 如果我们确定了一个传统变量的值, 那么下一次去"观察"它, 它还是这个值, 永远不会变, 比如 $x$ 为 $6$ 面骰子的面数. 那么无论我如何投掷这个骰子, $x = 6$ 是不会变的(别杠, 假设骰子不会被投裂开).
而随机变量的值是随机的, 不是确定的, 他可能有一些取值, 比如一个 $6$ 面的骰子, 点数可能为 $1, 2, 3, 4, 5, 6$, 投掷一次向上点数是多少就记为得分是多少, $X$ 为投掷一次的得分, $X$ 就是一个随机变量, 他的可能取值是 $X = \{1, 2, 3, 4, 5, 6\}$. 如果投掷一次, 得到的值是 $1$, 我们不能够说明, 投掷一次, 我的得分是 $1$. 每次投掷, $X$ 都随机取值. 具体取哪个值的概率是多少, 这就涉及到分布问题了, 这里不讨论.
期望
期望简单理解是随机变量的"加权平均", 即这个人尽皆知的公式 $E(X) = \sum P_iX_i$. 比如 $X$ 是投掷一个 $6$ 面的均匀骰子, 向上为多少点, 就得多少分, $X$ 是投掷一次的得分. 那么 $E(X) = \frac{1+2+3+4+5+6}{6} = 3.5$.
之前的误区
以前的理解是把随机事件拿来算期望了, 所以一直搞不明白. 还是拿上面的骰子举例, 以前理解的是, 投掷一次向上的点数为 $X$, 投掷一次向上的点数期望 $E(X) = 3.5$. 但"投掷一次向上的点数为 $X$“是一个"事件”, 他并不是随机变量, 无法加和, 更没有期望一说. 只有把随机事件映射到随机变量上, 才能够通过对随机变量进行期望计算, 从而估计随机事件的某些性质.
期望的线性性质
大概是两个方面, 一个是 $E(\alpha X) = \alpha E(X)$, 另一个是一直理解不能的这个东西 $E(X + Y) = E(X) + E(Y)$.
第一个就不展开了, 主要弄明白第二个的含义. 举个例子, 还是那个骰子, 投掷第一次的得分是一个随机变量 $X$, 投掷第二次的得分是一个随机变量 $Y$. 投掷两次的得分是一个随机变量 $Z$. 显然, 根据"变量的运算", 有 $Z = X + Y$. 用公式展开算一下就有 $E(Z) = E(X) + E(Y)$. 然后关于 $X + Y$ 的含义, 就是两个变量的值相加而已. 还是纠正一下误区 $X, Y$ 是随机变量, 而不是一个"事件", 所以并不是什么 $X$ 发生同时 $Y$ 发生, 根本不是同一个概念. 再来一个例子. 我投掷一个骰子, 向上的点数记为分数, $X$ 为我投掷一次的得分; 我对天开一枪, 打死几个人得几分, $Y$ 为我开一次枪获得的分数. 我现在有 $\frac{1}{3}$ 的概率要投掷一次骰子, $\frac{2}{3}$ 的概率开一次枪, $Z$ 为我这么做这个事件对应的得分, 那么 $Z = \frac{1}{3}X + \frac{2}{3}Y$, 所以我这么做的期望得分为 $E(Z) = E(\frac{1}{3}X + \frac{2}{3}Y) = \frac{1}{3}E(X) + \frac{2}{3}E(Y)$.
期望DP
搞清楚随机变量和期望的线性性质后, 再来看期望DP到底是个什么东西.
由于DP是个DAG, 所以我就直接画DAG了.
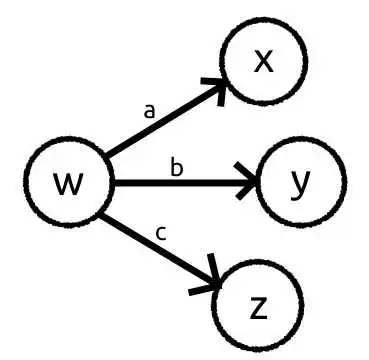
设 $dp(i)$ 表示从 $i$ 出发, 到终点的期望花费.
假设我们现在要算 $dp(w)$. 先明确随机事件, 从 $w, x, y, z$ 出发, 到终点的路径是一个随机事件(共四个随机事件), 从 $w$ 出发的这个随机事件可以被分成三个随机事件, 即, 从 $w$ 出发, 经过花费为 $a, b, c$ 的边到 $x, y, z$, 再到终点的路径. 然后设置对应的随机变量. 设随机变量 $W, X, Y, Z$ 分别为"从 $w, x, y, z$ 出发, 到终点的花费", $A, B, C$ 分别为 “从 $w$ 出发, 经过花费为 $a, b, c$(这些都是常量) 的边到点 $x, y, z$, 然后到终点的花费”, 显然有 $A = a + X, B = b + Y, C = c + Z$. 假设去点 $x, y, z$ 的概率分别为 $P_x, P_y, P_z$(这些都是常量), 从 $w$ 出发这个随机事件拆成的三个随机事件不可能同时发生, 即一次只能走一条边, 所以
$$\begin{aligned} W &= P_x \cdot A + P_y \cdot B + P_z \cdot C \\ &= P_x(a + X) + P_y(b + Y) + P_z(c + Z) \end{aligned}$$
重点来了, 根据期望的线性性质, 有
$$\begin{aligned} E(W) &= E\left(P_x(a + X)\right) + E\left(P_y(b + Y)\right) + E\left(P_z(c + Z)\right) \\ &= P_x(a + E(X)) + P_y(b + E(Y)) + P_z(c + E(Z)) \end{aligned}$$
也就是:
$$dp(w) = P_x(a + dp(x)) + P_y(b + dp(y)) + P_z(c + dp(z))$$
这玩意就是转移方程了.
特别地, $a = b = c, P_x + P_y + P_z = 1$, 再化简一下则有,
$$dp(w) = 1 + \sum_{v \in {x, y, z}} dp(v)$$
也就是之前写了个🔨的东西
例题
Boxes
推一下就显然只需要用第一次提示, 然后无论开出来的是什么, 后面都知道有多少个黑的多少个白的了. 然后排序, 显然先开代价小的.
假设当前 $dp$ 在 $i$, 我们要考虑的是这样的一个随机事件: $[i, \dots, n]$ 这 $n-i+1$ 个盒子里球的状态. 状态可以用长度为 $n-i+1$ 的 01 串表示黑白, 并且这个状态是随机的, 也就是随机事件成立. 这个随机事件能够"递推", 把可能发生的事件这样分组: $\{0 + [000\dots00, 000\dots01, 000\dots11, \dots, 111\dots11], 1 + [000\dots00, 000\dots01, 000\dots11, \dots, 111\dots11]\}$(这里$+$是字符串连接). 也就是当前 $i$ 可能是 01, 接上后面随机事件 $[i+1, \dots, n]$ 的状态的可能事件. 然后设置随机变量, 设 $W$ 为盒子 $[i, \dots, n]$ 的状态对应的代价, 根据随机事件的"递推过程", 首先再设几个随机事件和随机变量, 随机变量 $X_{0/1}$ 为随机事件后面状态全0或全1, 对应的代价, 随机变量 $Y$ 为随机事件后面状态非全0和非全1, 对应的代价, 随机变量 $Z$ 为随机事件后面状态对应的代价. 后面是全0或全1, 与后面非全0并且非全1, 这两个随机事件是不可能同时发生的, 并且, 把这整个随机事件看成一个"事件", 这两个"事件"发生的概率很容易求, 而且这两个"事件"带上他们的分布概率, 就是后面状态这个随机事件了. 体现在随机变量上就是 $Z = P(\text{后面全0})X_0 + P(\text{后面全1}X_1 + P(\text{后面非0非1})Y)$. 同理我们把 $[i, \dots, n]$ 的状态这个随机事件, 再多拆一点, 当前是0, 当前是1, 后面是全0或全1, 后面是非全0并且非全1, 组合一下就是 $2 \times 3$ 个"事件", 这些"事件"以及他们发生的概率的综合, 就是这个随机事件了. 全是同一个颜色不需要开当前的, 否则需要开当前的, 开当前的代价设为 $w_i$, 根据随机事件对应的随机变量, 有:
$$\begin{aligned} W = &P(\text{当前是0})P(\text{后面全0})X_0 + \\ &P(\text{当前是1})P(\text{后面全1})X_1 + \\ &P(\text{当前是0})P(\text{后面全1})(X_1 + w_i) + \\ &P(\text{当前是1})P(\text{后面全0})(X_0 + w_i) + \\ &P(\text{当前是0})P(\text{后面非全0非全1})(Y + w_i) + \\ &P(\text{当前是1})P(\text{后面非全0非全1})(Y + w_i) \end{aligned}$$
然后化简一下这一大坨东西, 就可以得到:
$$W = Z + (1 - (P(\text{当前是0})P(\text{后面全0}) + P(\text{当前是1})P(后面全1))) \cdot w_i$$
设 $p_i$ 为 $w_i$ 前面的系数(即某种特定事件发生的概率), 这个 $p_i$ 是可以计算的, 且是一个常量. 那么 $W = Z + p_iw_i$, 再根据期望的线性性质, 有 $E(W) = E(Z) + p_iw_i$. 然后设 $dp(i)$ 为 $[i, \dots n]$ 的状态期望的代价, 这样就有 $dp(i) = dp(i+1) + p_i w_i$, 转移即可.
后感?
考场上是考虑后面的具体状态, 然后写出了正确的转移方程(但是出了亿点sb问题最后没过), 只不过当时不清楚"随机事件"和"随机变量"这些概念. 如果明确了这些概念, 之后做题应该要有的放矢, 而不是瞎猫撞见死耗子.
总结
写得不是很好, 边写边发现应该再写上随机事件的, 因为随机事件能够"递推"是期望dp能够做的本质原因. 咕咕咕. 心情好可能重写, 反正自己应该大概是理解了叭?
第二天一大早起来就改了,,,
在做期望dp的时候, 首先应该去找随机事件, 并根据题目设随机变量, 然后通过随机事件之间可能存在的"递推关系", 找随机变量之间的线性关系, 最后再用dp推算随机变量的期望, 而不是一上手就设dp为啥啥啥的. 可能熟练了就可以一步到位? 反正我这么菜, 还是用笨办法一步一步来叭. 之后如果碰到题, 试试这种按部就班的方法去搞, 再来往例题里加, 先这样, 写快 3h 了, 溜了.