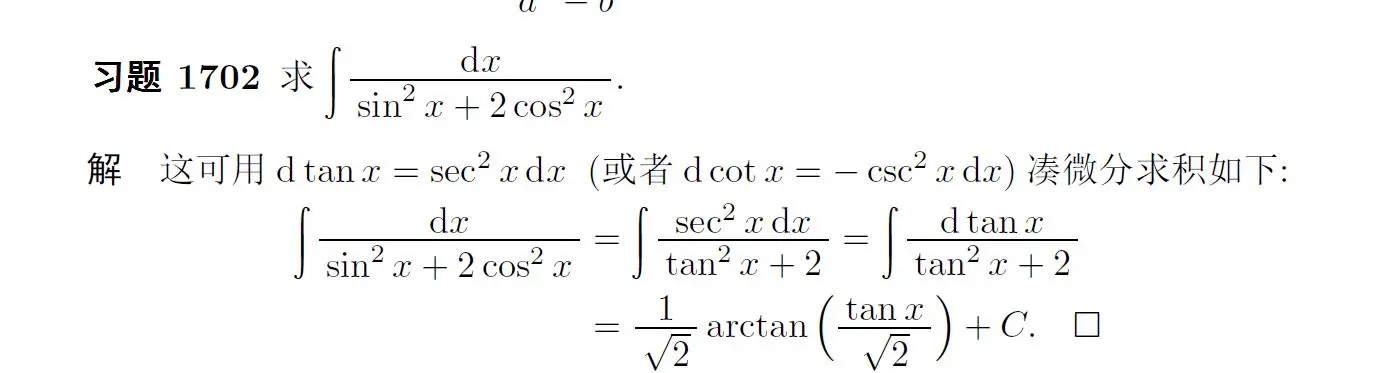积分的各种淫奇技巧
积分好难 😖
基本积分表
标记 (*) 的是不熟的, 需要加强记忆.
最基本
这是我自己认为的最基本, 和教材上不太一样
一定要记住啊!!!
幂指对
- $\int kdx = kx + C$
- $\int x^\mu dx = \frac{x^{\mu + 1}}{\mu + 1} + C \ \ (\mu \ne -1)$
- $\int \frac{dx}{x} = \ln |x| + C$
- $\int e^x dx = e^x + C$
- $\int a^x dx = \frac{a^x}{\ln a} + C$
三角
- $\int \sin xdx = -\cos x + C$
- $\int \cos xdx = \sin x + C$
- $^* \int \tan xdx = -\ln |\cos x| + C$
- $^* \int \cot xdx = \ln |\sin x| + C$
- $^* \int \sec ^2 xdx = \tan x + C$
- $^* \int \csc ^2 xdx = -\cot x + C$
- $^* \int \sec x \tan x dx = \sec x + C$
- $^* \int \csc x \cot x dx = -\csc x + C$
反三角
- $\int \frac{dx}{1 + x^2} = \arctan x + C$
- $\int \frac{dx}{\sqrt{1 - x^2}} = \arcsin x + C$
再记一点
忘记了的话可以用换元法由最基本积分推导
含有$\frac{1}{\pm x^2 \pm a^2}$
- $\int \frac{dx}{a^2 + x^2} = \frac{1}{a} \arctan \frac{x}{a} + C \ \ $ (第一类换元)
- $^ * \int \frac{dx}{x^2 - a^2} = \frac{1}{2a} \ln |\frac{x-a}{x+a}| + C \ \ $ (拆$\frac{1}{x^2 - a^2} = \frac{1}{2a}(\frac{1}{x-a} - \frac{1}{x+a})$, 再第一类换元)
- $^ * \int \frac{dx}{a^2 - x^2} = \frac{1}{2a} \ln |\frac{a+x}{a-x}| + C \ \ $ (拆$\frac{1}{a^2 - x^2} = \frac{1}{2a}(\frac{1}{a-x} + \frac{1}{a+x})$, 再第一类换元, 或者直接等于上面公式的相反数)
割
- $\begin{aligned} \int \sec xdx &= \frac{1}{2} [\ln (1 + \sin x) - \ln (1 - \sin x)] + C \\ ^ * &= \ln |\tan (\frac{x}{2} + \frac{\pi}{4})| + C \\ ^ * &= \ln |\sec x + \tan x| + C \end{aligned}$
- $\begin{aligned} \int \csc xdx &= -\frac{1}{2} [\ln (1 + \cos x) - \ln (1 - \cos x)] + C \\ ^ * &= \ln |\tan \frac{x}{2}| + C \\ ^ * &= \ln |\csc x - \cot x| + C \end{aligned}$
以$\int \sec xdx$为例, 写一下过程:
$\begin{aligned} \int \sec xdx &= \int \frac{dx}{\cos x} \\ &= \int \frac{\cos xdx}{\cos^2 x} \\ &= \int \frac{d\sin x}{1 - \sin^2 x} \\ &= \frac{1}{2} [\ln (1 + \sin x) - \ln (1 - \sin x)] + C \end{aligned}$
$\begin{aligned} \int \sec xdx &= \int \frac{(\sec xdx)(\sec x + \tan x)}{\sec x + \tan x} \\ &= \int \frac{(\sec^2 x + \sec x \tan x)dx}{\sec x + \tan x} \\ &= \int \frac{d(\sec x + \tan x)}{\sec x + \tan x} \\ &= \ln |\sec x + \tan x| + C \end{aligned}$
以上过程用到第一类换元
含有$\frac{1}{\sqrt{\pm x^2 \pm a^2}}$
- $^ * \int \frac{dx}{\sqrt{a^2 - x^2}} = \arcsin \frac{x}{a} + C \ \ $ (三角换元$x = a\sin t$, 再第一类换元)
- $^ * \int \frac{dx}{\sqrt{x^2 - a^2}} = \ln |x + \sqrt{x^2 - a^2}| + C \ \ $ (三角换元$x = a\sec t$, 再第一类换元)
- $^ * \int \frac{dx}{\sqrt{x^2 + a^2}} = \ln |x + \sqrt{x^2 + a^2}| + C \ \ $ (三角换元$x = a\tan t$, 再第一类换元)
双曲(暂时没用过)
- $\int \sinh xdx = \cosh x + C$
- $\int \cosh xdx = \sinh x + C$
积分方法
第一类换元
凑微分法
凑微分法是复合求导的逆运算.
先来看看复合求导:
$$[f(g(x))]’ = f’(g(x))g’(x)$$
那么第一类还原法就是看被积函数是不是长成上述式子右边的样子, 或能不能转化成右边. 如果可以, 那么把$g’(x)$放到积分号里面.
一般来说, 我们只需要找到$g’(x)$和$g(x)$以及$f’(g(x))$即可. 所以, 我们有两个思考方向:
1. 找$f’(g(x))$.
虽然这里有一个$g(x)$, 看起来比较难找, 但是我们_忽略_他, 只要找一个最大的函数, 就是$f’(u)$.
这个$f(u)$一般有如下的形式:
- $e^u$, 即$e^{g(x)}$, 比如$e^{\sin x}, e^{x^2}, e^{\arcsin x}, \dots$
- 三角函数, 比如$\sin 2x, \tan e^x$
- $\frac{1}{u}$, 即$\frac{1}{g(x)}$, 比如$\frac{1}{1+x}, \frac{1}{\cos x}, \dots$
- $u^{\alpha}$, 即$g(x)^{\alpha}$, 比如$\sqrt{\frac{1}{x}}, \dots$
而且, $f’(u)$是被积式子的某一部分, 而且是这一部分的最外层函数. 根据这两条性质, 结合一些经验, 有时是一眼能看出$f’(u)$的.
注意, $f’(u)$只是一部分, 还有一个$g(x)$呢! 所以, 被积式子的最外层函数不是$f’(u)$
2. 找$g(x)$
找$g(x)$的方法比较无脑, 凭经验或直觉拿一个式子出来, 求导, 倒数是不是剩下部分的某一组成(通常还需要凑一下系数), 如果是, 则找到了.
而如果式子中出现了积分表中的内容, 那么一眼就能看出$g(x)$来.
例题
$$\int \sqrt{ \frac{\ln (x + \sqrt{1 + x^2})} {1 + x^2} }dx$$
下面分别用三种方法来尝试解决
1. 找$f’(u)$
可以把分子分母看成两个部分, 猜想$f’(u)$为$\sqrt{u}$, 那么$g(x)$为$\ln (x + \sqrt{1 + x^2})$, $g’(x)$为$\frac{1}{\sqrt{1 + x^2}}$, 验证一下是对的, 就恰好找到了.
如果猜想了一个$f’(u)$, 得到g(x)和g’(x), 但是他们并不是导数关系, 那就是f’(u)找的不合理
2. 找$g(x)$
$\ln (x + \sqrt{1 + x^2})$长得太奇怪了, 对他求个导, 欸, 刚好是$\frac{1}{\sqrt{1 + x^2}}$, 找完了.
如果对公式熟悉的话, 很容易看出来$\ln (x + \sqrt{1 + x^2})$是这个公式的右边:
$$\int \frac{dx}{\sqrt{x^2 + a^2}} = \ln |x + \sqrt{x^2 + a^2}| + C$$
逆代换法
逆代换法是用某个可微函数$x=\phi(t)$代入到被积表达式$f(x)dx$中, 于是得到
$$\int f(x)dx = \int f(\phi(t))\phi’(t)dt$$
对变换过的式子积分, 然后代回$t = \phi^{-1}(x)$
根式代换
根式下如果是一个一次函数, 或者是两个一次函数的比值, 那么我们可以尝试令$t = \sqrt{g(x)}$, 得到$x = G^{-1}(t)$, 用这两个换元代入积分式子.
第二类换元
第二类换元法就是把$x$换掉, $x = \psi(t)$, 求积分, 然后把结果中的$t$再换成$\psi^{-1}(x)$.
三角换元
碰到$\pm x^2 \pm a^2$ 或 $\sqrt{\pm x^2 \pm a^2}$的式子可以考虑三角换元, 即:
- $a^2 - x^2 \Longrightarrow x = a\sin t$
- $a^2 + x^2 \Longrightarrow x = a\tan t$
- $x^2 - a^2 \Longrightarrow x = a\sec t$
由于使用三角换元, 结果中可能会出现不同名的关于$t$的三角函数, 此时我们根据边和角的关系画一个直角三角形, 把各名字的三角函数在三角形上用比的形式写出来, 就可以方便地代回去了.
例题
咕咕咕
倒代换
当分母次数高于分子时(一般高两次以上), 可以尝试倒代换, 令$x = \frac{1}{t}$, 可以消去分母.
例题
咕咕咕
部分积分
有理函数积分
易错点总结
- 当用凑微分法进行第一类换元时, 如果凑进去的$g(x)$的$x$有系数, 那么凑进去的时候外面要除以这个系数. 如 $\int (a-x)dx = -\int (a-x)d(-x) = -\int (a-x)d(a-x)$, 以及$\int \cos 2x dx = \int \frac{1}{2} d\sin 2x$. 如果怕出错, 可以再求导回去看看是不是对的.
- $\int \frac{dx}{a^2 + x^2} = \frac{1}{a} \arctan \frac{x}{a} + C$ 有系数$\frac{1}{a}$, 而$\int \frac{dx}{\sqrt{a^2 - x^2}} = \arcsin \frac{x}{a} + C$ 没有系数!!! 注意不要记混了!!!
- 当从根号中提出来$x$时, 注意讨论$x<0$的情况. 只需要对$x>0$的情况求完以后, 令$t = -x$再推一下即可.
一些技巧
突然出现很高次的幂
$x^\alpha$: 换元$u = x^\alpha$
$$\int \frac{dx}{x(x^6+4)}$$
$$u = x^6$$ $$du = dx^6 = 6x^5dx \Rightarrow dx = \frac{du}{6x^5}$$ $$\therefore \int \frac{dx}{x(x^6+4)} = \frac{1}{6} \int \frac{du}{x^6(x^6+4)} = \frac{1}{6} \int \frac{du}{u(u+4)}$$
不同函数, 三角高次: 降幂
$$\int x\cos^2 xdx$$
$$\int x\cos^2 xdx = \frac{1}{2} \int x(\cos 2x + 1)dx$$
分母有$\sqrt{1+g^2(x)}$
提出$g(x)\sqrt{\frac{1}{g^2(x)} + 1}$, 用$\frac{1}{g(x)}$凑微分

分母为高次三角函数和
考虑同时除以$\cos x$, 得到$\tan x$和$\sec^2 x$, 利用$\int \sec^2 x = \tan x$进行凑微分
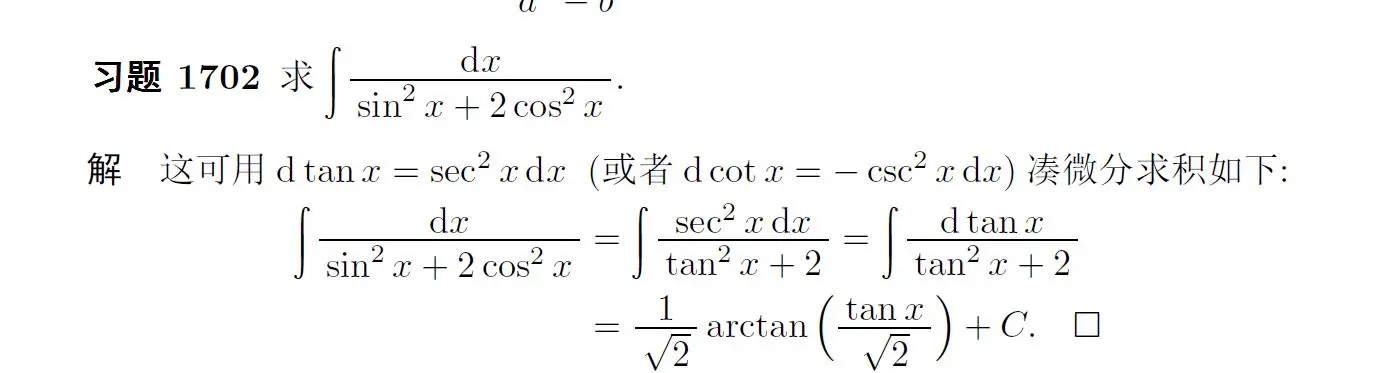
分母为高次三角函数积
将分子用$1 = \sin^2 x + \cos^2 x$化成和分母次数接近, 然后直接拆成关于三角函数的有理分式之和; 或者分子分母同时乘某个三角函数, 然后分子凑微分

板刷经典题