超详细拉格朗日插值法
本来是多项式里的内容, 学完后发现好多啊, 于是独立成文.
拉格朗日插值
拉格朗日公式如下:
$$L(x) = \sum_{i=0}^{n-1} y_i \frac{\prod \limits_{j \ne i} (x - x_j)}{\prod \limits_{j \ne i} (x_i - x_j)}$$
这个公式的意思是, 根据 $n$ 个点计算的 $n-1$ 次($n$ 次数界)多项式为 $L(x)$
有个大佬用通俗易懂的方法解释了这个公式, 我直接copy. (其实是我看不懂crt方法的证明)
下文引自 拉格朗日插值法入门 @crashed 大佬下标 $1 \sim n$, 我这里下标 $0 \sim n-1$, 注意一下.
它的思想非常简单, 大概可以理解为——硬性配凑！
怎么配凑呢？我们举个例子, 平面上有三个点, $(x_1,y_1),(x_2,y_2),(x_3,y_3)(x_1<x_2<x_3)$, 我们现在用它们仨插值.
根据小学基础知识, 我们知道, 这三个点肯定可以唯一确定一个二次函数.
那么我们就尝试找到它, 怎么找？拉格朗日想到了一个比较粗暴的方法——咱对于每个点都搞一个子函数 $f_i(x)$, 要求 $f_i(x)$ 在 $x = x_i$ 的时候得到 $1$, 在 $x = x_j(j \ne i)$ 的时候得到 $0$, 把 $n$ 个子函数凑起来, 得到的函数不就过了 $n$ 个点了!
也就是说, 我们要计算 $n$ 个子函数, 第 $i$ 个子函数为:
$$f_i(x)= \begin{cases} 1 & x=x_i\newline 0 & x=x_j(j\not=i)\newline I\ don’t\ care & otherwise \end{cases}$$
那么插值的结果就是:
$$f(x)=\sum_{i=1}^n y_if_i(x)$$
回到原问题上面来. 考虑构造 $f_1(x)$, 对于 $f_1(x_j) = 0 (j >1 )$ 的情况很好满足, 可以想到:
$$f_1(x) = (x - x2) (x - x3)$$
怎么让 $f_1(x_1) = 1$ 呢? 我们只需要把不用的丢掉就好:
$$f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}$$
所以最后就有 $f_1(x)$ 长成下面这个亚子:
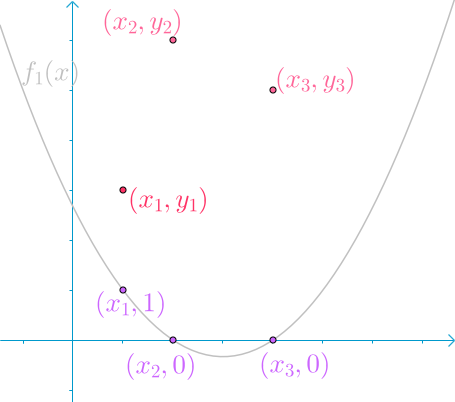
同理构造出 $f_2(x)$:
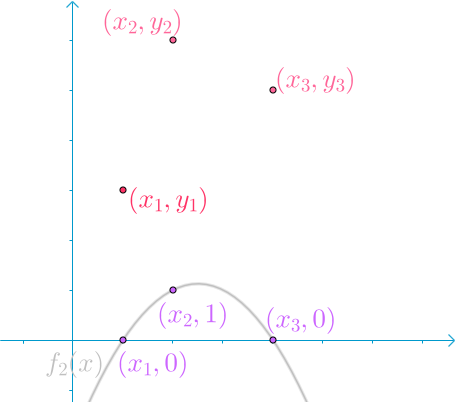
和 $f_3(x)$:
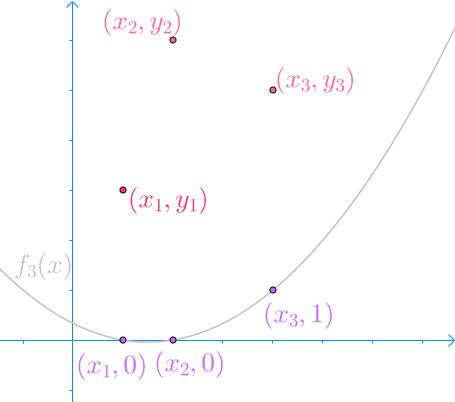
求和得到 $f(x)$:
$$f(x)=\frac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+\frac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+\frac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}$$
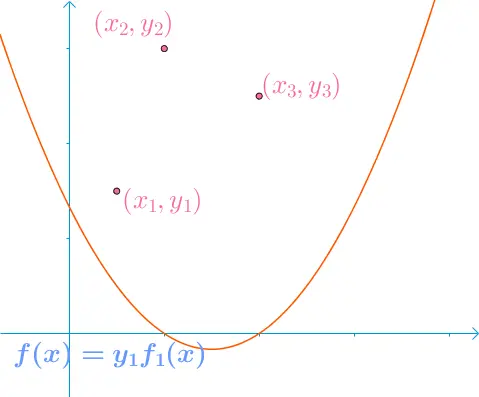
也可以很方便地推广到一般形式: 对于 $n$ 个点 $(x_1,y_1),(x_2,y_2),…,(x_n,y_n)(x_1<x_2<…<x_n)$, 设:
$$f_i(x)=\frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)}$$
那么插值结果就是:
$$f(x)=\sum_{i=1}^ny_if_i(x)=\sum_{i=1}^ny_i\times \frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)}$$
$\prod \limits_{j \ne i} (x - x_j)$ 决定了 $L(x)$ 的次数, 一共有 $n-1$ 个形如 $(x - k)$ (视 $x_j$ 为常数 $k$) 的东西相乘, 那么它就是 $n-1$ 次多项式($n$ 次数界多项式).
这个公式可以这样记录:
$$L(x) = \sum_{i=0}^{n-1} y_i \ell_i(x)$$ $$\ell_i(x) = \prod_{j=0,j\ne i}^{n-1} \frac{(x - x_j)}{(x_i - x_j)} = \frac{(x - x_0) \cdots (x - x_{i-1})(x - x_{i+1}) \cdots (x - x_{n-1})}{(x_i - x_0) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_{n-1})}$$
其中 $\ell_i(x)$ 称为拉格朗日基本多项式.
有了这个公式, 我们虽然不能直接求出多项式的系数, 但是能够直接求出 $L(x)$ 的值, 也就是 $n$ 个点确定的多项式 $L(x)$, 在任意点 $\xi$ 处的值 $L(\xi)$. 看这个公式, 两重循环, 所以复杂度是 $O(n^2)$ 的.
|
|
计算多项式系数
虽然根据这个拉格朗日插值公式不能直接计算系数, 但是有间接计算的方法, 复杂度是 $O(n^2)$ 的. 算法导论上有习题. 先咕咕钴, 碰到再说.
当 x 连续时的优化
如果点值表示中 $n$ 个点的横座标 $x$ 是连续的, 那么可以把求 $L(\xi)$ 优化到 $O(n)$. 这也是拉格朗日插值法的常见考点(因为复杂度高于 $O(n\log n)$ 就可以直接 FFT 了, 要拉格朗日插值何用).
很明显, 这里主要优化的是 $\ell_i(x)$ 的计算.
$$\ell_i(x) = \frac{(x - x_0) \cdots (x - x_{i-1})(x - x_{i+1}) \cdots (x - x_{n-1})}{(x_i - x_0) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_{n-1})}$$
对不同的 $i$, 分子其实是有很多重复的部分的. 对于要求的值 $x = \xi$, $O(n)$ 预处理前缀积和后缀积, 即 $pre_i(\xi) = \prod_{j=0}^i (\xi - x_j)$, $suf_i(\xi) = \prod_{j=i}^{n-1} (\xi - x_j)$, 这样每次求 $\ell_i(\xi)$ 的分子, 就是 $O(1)$ 的了.
再考虑分母, 因为 $x_i$ 连续, 不妨设 $x_i < x_{i+1}$, 那么对于前一半, 即 $(x_i - x_0) \cdots (x_i - x_{i-1})$, 就是个阶乘 $(x_i - x_0)!$; 对于后一半来说, 先把每一项都取相反数, 变成 $(x_{n-1} - x_i) \cdots (x_{i+1} - x_i)$, 这也是个阶乘 $(x_{n-1} - x_i)!$, 然后再看对多少项取了相反数, 也就是说, 分母需要乘以 $(-1)^{n-1-i}$. 阶乘可以 $O(n)$ 预处理.
那么最后 $\ell_i(x)$ 可以 $O(1)$ 计算
$$\ell_i(x) = \frac{pre_{i-1}(x) \cdot suf_{i+1}(x)}{(-1)^{n-1-i}(x_i - x_0)! (x_{n-1} - x_i)!}$$
$L(x)$ 就可以 $O(n)$ 计算了.
(没有找到很板的板题)
多项式的前缀和
令 $S(x) = \sum_{i=0}^{x} A(i)$, 称 $S(x)$ 为 $A(x)$ 的(离散)前缀和. $S(x)$ 是一个多项式, 用点值表达的解释如下(其实是我看不懂数学推导):
假设有 $A(x)$ 是 $n$ 次数界多项式, 那么它可以由点 $(i, A(i)), i \in [0, n]$ 表示. 考虑 $S(x)$ 的点值表示为 $(i, S(i)) = (i, \sum_{j=0}^i A(j))$. 这样"对点做前缀和"得到的点, 就是点值表示的多项式 $S(x)$ 了.
需要注意的是, $n$ 次数界多项式的离散前缀和是一个 $n+1$ 次数界的多项式. 这里有一个简单理解(其实是我看不懂差分前缀和母函数者伯努力什么的):
在做前缀和的时候, 默认第一个点的前一个点($-1$?)的值是 $0$, 如果它不是 $0$, 那么答案显然不一样. 也就是说, 这里还有一个点. 这 $n+1$ 个点, 才能确定唯一一个 $n+1$ 次数界多项式.
计蒜客-40254 2019ICPC南昌邀请赛B.Polynomial
|
|
CF-622F The Sum of the k-th Powers
|
|
拉格朗日基本多项式与多项式线性空间
一组 $\vec x$ 可以确定一组 $\vec l$, 那么对于不同的 $\vec y$, 可以看成是 $\ell_i$ 的不同系数. 所以可以把它看成多项式线性空间, 即 $L = \sum y_i \ell_i$. 好玩的东西在于, $\vec l$ 是线性无关的, 证明如下:
即证明, 仅有系数 $y_i$ 全为 $0$ 时, $L = 0$ (多项式线性空间下的 $\vec 0$ 等于数值 $0$). 设 $L = \sum y_i \ell_i = 0$, 有 $\forall \xi L(\xi) = 0$ , 因为 $L(x_i) = y_i$, 所以 $y_i = 0$. 证毕.
也就是说, 基本多项式 $\ell_i$ 一定是它张成的多项式线性空间的一组基底.
虽然目前不知道有什么用但是感觉好奇秒啊
并没有找到题, 但是我想到一个, 先不说, 看看之后能不能参与一波出题工作QwQ
重心拉格朗日插值法
改进版拉格朗日插值法
也称重心拉格朗日插值法第一型
对于已经计算过的点 $L(\varepsilon)$, 如果这个时候添加(或者删除)一个点值 $(x_k, y_k)$, 要重新求 $L(\varepsilon)$ 的话是 $O(n^2)$ 的. 对公式进行变形, 预处理一些东西, 能够做到 $O(n)$.
先对 $\ell_i(x)$ 变个形:
$$\begin{aligned} \ell_i(x) &= \frac{\prod_{j \ne i} (x - x_j)}{\prod_{j \ne i}(x_i - x_j)} \\ &= \frac{\prod_{j=0}^{n-1}(x - x_j)}{(x - x_i)} \cdot \frac{1}{\prod_{j \ne i}(x_i - x_j)} \end{aligned}$$
可以看到, 第一个分式的分子是和 $i$ 无关的东西, 令它为 $\ell(x) = \prod_{j=0}^{n-1}(x - x_j)$, 同时令 $w_i = \frac{1}{\prod_{j \ne i}(x_i - x_j)}$ (分母是 $\ell_i(x)$ 第二个分式的分母), 那么有
$$\ell_i(x) = \frac{\ell(x)w_i}{x - x_i}$$
其中, $w_i$ 称为重心权. 那么 $L(x)$ 就可以化为:
$$\begin{aligned} L(x) &= \sum_{i=0}^{n-1} y_i\ell_i(x) \\ &= \ell(x) \sum_{i=0}^{n-1}\frac{w_iy_i}{x - x_i} \end{aligned}$$
以增加点为例, 先 $O(n)$ 求 $\ell(x)$, 然后对 $O(n)$ 个 $w_i$ 在 $O(1)$ 内修改, 然后 $O(n)$ 求新增的一个 $w_k$, 最后 $O(n)$ 计算 $L(x)$.
重心拉格朗日插值法
也称重心拉格朗日插值法第二型
对一个 $n$ 次数界多项式 $g(x) \equiv 1$ 取 $n$ 个点, 进行改进版拉格朗日插值, 可以得到:
$$g(x) = \ell(x)\sum_{i=0}^{n-1} \frac{w_i}{x - x_i}$$
然后进行神奇的多项式除法, 得到
$$L(x) = \frac{L(x)}{g(x)} = \frac{\sum_{i=0}^{n-1}\frac{w_i}{x-x_i}y_i}{\sum_{i=0}^{n-1}\frac{w_i}{x-x_i}}$$
这个公式可以少维护一个 $\ell(x)$, 不过好像差不太多…
|
|