计算机网络 - 物理层
寄!
信号
模拟信号
简单信号: 一个正弦波
复合信号: 多个不同频率, 相位, 振幅的正弦波叠加
任何复合信号都可以被 分解 成多个不同频率, 相位, 振幅的正弦波叠加. 就像任意函数总能用多项式函数拟合一样
周期信号分解出的正弦波 频率离散; 非周期信号分解出的正弦波 频率连续
一个周期为 $T$ 的复合信号, 分解出的正弦波周期为 $\frac{T}{k}, k \in \mathbb{Z}_+$ (逆过来考虑?). 非周期信号可以看成周期无穷大, 故无穷多个简单信号频率连续.
与复合信号周期对应的频率称为 基础频率, 具有基础频率的正弦波称为 第一谐波, 其余频率为第一谐波 $k$ 倍的正弦波称为第 $k$ 谐波
频域图
一个正弦波:
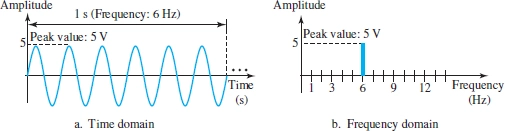
简单信号在频域图上是一条线 (个点), 周期复合信号是离散多条线 (个点), 非周期复合信号是连续的多条线 (个点) (一般画包络面).
带宽
复合信号的频率范围, 最大频率减去最小频率
数字信号
若一个 电平 可以表示 $k$ 位, 则需要 $2^k$ 个电平
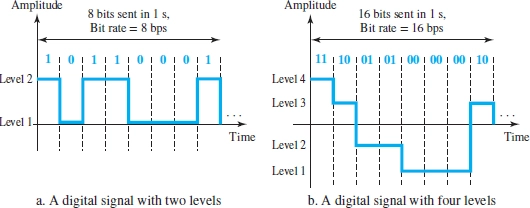
比特率
1s 内发送的位数 (不是电平数). 单位 bps
频域
数字信号可以分解, 其中, 水平的部分频率为 0, 垂直部分频率为无穷大. 分解以后得到频率离散 (周期性) 或连续 (非周期性) 的频域图. 这说明了数字信号的带宽无穷大.
传输
基带 传输
低通通道, 不转换成模拟信号
宽带宽的几乎可以传输整个信号
有限带宽则需要近似一下
大致近似
假如使用正弦波, 大于 0 的部分为 1, 小于 0 的部分为 0. 则传输 101010… 这样的序列, 可以用一个简单的正弦波代替. 其中, 10 是一个小周期, 于是在 1s 内传输长度为 N 的这样的序列, 需要有 $\frac N 2$ 个周期. 也就是这个正弦波的频率为 $\frac N 2$. 而其他的序列, 无论如何频率都不会超过 $\frac N 2$. 于是通过这种方法近似, 所需要的最大频率是 $\frac N 2$. 而频率从 0 开始, 所以所需带宽为:
$$B = \frac N 2 - 0 = \frac N 2$$
更好近似
大致近似算出来的带宽, 是 能够分辨出哪里是 0 哪里是 1 所需要的最小带宽. 加入更高频率的信号, 可以更准确拟合数字信号. (想象加入无穷大频率的信号, 那么就变成了这个数字信号本身了)
使用最高频率为第 $k$ 谐波 ($f = \frac{kN}2$), 可以拟合得更好. 相应地带宽变为 $\frac{kN}2$.
宽带 传输
转换成模拟信号, 传输, 接收到以后转换会数字信号
若转换后的信号不要求频率从 0 开始, 则传输介质不必是低通的
传输损耗
衰减
能量衰减, 表现为功率 (振幅) 降低.
分贝
使用分贝来衡量功率的变化
$$dB = 10 \log_{10} \frac{P_2}{P_1}$$
分贝正为变大, 负为变小.
把线的损耗抽象成 减小器 (对应放大器), 节点之间的放大/衰减用分贝衡量可以直接相加.
失真
不同频率的分信号在介质中有不同的传播速率, 就像不同颜色的光在介质中的传播速率不同一样.
传播了一段时间后, 信号的形状发生改变
噪声
信噪比, 平均信号功率比上平均噪声功率. 可用分贝衡量.
数据速率限制
- 有效带宽
- 使用电平数
- 噪声
奈奎斯特比特率
$$N = 2B\log L$$
和基带传输大致近似的比特率一样, 只不过代入更多的电平数, 得到更通用的结果 (虽然再用之前的方法推一遍会感觉推不出来)
香农容量定理
$$C = B \log (1 + SNR) = B\frac{SNR_{dB}}{3}$$
$SNR$ 很大, 近似 $1 + SNR = SNR$, 可推得右式
性能
带宽 (以比特率衡量)
介质所能传递的最大比特率
吞吐量
介质实际传递的比特率
延迟
- 传播时间: 一位在两地之间的传播时间, $T_p = \frac s v$
- 传输时间: 开始传递第一位和最后一位的间隔时间 $T_p = \frac l B$
- 排队时间
- 处理延迟
带宽与延迟的乘积
链路同时存在的最多位数
抖动
时间敏感的数据, 各个部分延迟不同导致收到后组合起来的报文与之前不同. 这个性能问题与延迟有关, 并且可以通过办法解决.
数字到数字编码
数字元素与信号元素
数字元素是位, 信号元素简单理解是电平, 一个电平可以对应多个位. 当然也可以将一系列电平组合编码成多个位. 信号速率称 波特率. 承载比率 $r$ 定义为一个信号元素承载的数字元素.
(使用调制的方法, 可能会将一个比特编码成多个电平信号, 或者使用压缩算法, 可以使多个数据编码成一个组长度更短的电平信号)
比特率是数据层面的东西, 波特率是物理层面的东西, 也就是说, 衡量数据物理传输的速率是波特率
$$S = \frac{cN} r$$
$c$ 是情况因子, 情况视不同数据因为调制和压缩而变化, 导致同样长度的 01 串可以使用不同长度的信号元素传递. 举个简单的例子, 连续的 0 可以压缩一下, 然后用小于其长度的信号元素传递, 而无规律的数据无法压缩.
所以, 带宽实际上是根据波特率而不是比特率决定的.
$$B_{min} = \frac{cN}r \Longrightarrow N_{max} = \frac{Br}c$$
编码时需要考虑的因素
- 基线偏移: 接收方计算收到的这组信号的功率均值, 作为 基线, 据此判断 0 和 1. 如果以高振幅编码为 1, 低振幅编码为 0, 则若接收到的数据都是 0 或者 1, 就会导致基线偏移, 从而可能错误解码.
- 直流成份: 电平恒定一段时间, 信号具有频率很低的 直流成分. 部分链路无法处理.
- 自同步: 时钟不同步, 可能解码错误. 编码中加入一些东西, 根据数据来 “同步” 时钟.
编码方案
每种编码方案都要分析上述三个因素
单极性编码 (不归零, NRZ)
单极性指的是电平要么正要么 0, 对应双极性还有负的电平.
不归零指的是, 数字信号表示 0 / 1 的时候, 没有 穿越 0.
NRZ-L
1 编码为高电平, 0 编码为低电平
NRZ-I
1 编码为电平反向, 0 编码为电平不反向
双相
曼彻斯特
1 编码为前半部分负电平后半部分正电平, 0 编码为前半部分正电平, 后半部分负电平.
差分曼彻斯特
1 编码为 与周期违背的反向, 0 编码为 与周期相同 (与书上的理解不同)
双极性
AMI
1 编码为正电平或者负电平, 并与上一个 1 相反, 0 编码为低电平
伪三元
与 AMI 相反, 0 正负高电平, 1 低电平
扰动
AMI 编码, 替换连续的 0 的扰动方案 (因为连续的 0 无法自同步)
B8ZS
00000000 -> 000VB0VB
V 表示违反 AMI 的 1, B 是相同的
HDB3
0000 -> 000V / B00V
保持非零脉冲偶数
传输模式
并行 传输
多条线, 同时传输
串行 传输
- 异步: 以字节发送, 前补 0 表示开始, 后补 1 表示结束, 用以同步. 间隔不理会. 慢
- 同步: 多个字节组成帧, 没有同步机制 (数据链路层负责同步), 帧间有间隔. 快
- 等时: 整个流同步
数字到模拟编码
以下举例均为信号元素数量为 2 的调制方法.
幅移键控 (ASK)
调制振幅
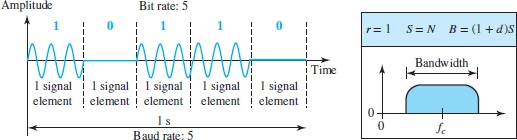
$f_c$ 是载波频率, 在带宽的中间. 调制可以移动带宽位置.
$B = (1 + d) S$, $d$ 是和调制解调器有关的因子, 会给出.
结合 $S = \frac N r = \frac{N}{\log L}$, 可以求其他参数.
(书上严谨地说, $L$ 是元素信号数量, 与之前的电平数量不同, 而调制是由数字信号转到了元素信号, 所以电平数量和信号数量是相等的. 此处只需要注意概念即可, 公式不变)
频移键控 (FSK)
调制频率
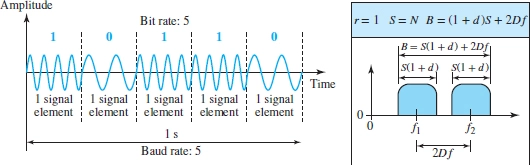
$B = (1 + d) S + 2 \Delta f$
可看成两个频率的 ASK, 则每个频率的带宽是 $(1 + d) S$. 中间可能有空的 (如图). $2 \Delta f = f_2 - f_1$.
相移键控 (PSK)
调制相位.
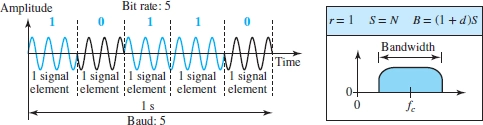
$B = (1 + d) S$
正交相移键控制 (QPSK)
两个正交的波进行调制然后相加, 可以得到 $2 \times 2$ 个信号元素, 提高载波利用率.
正交振幅调制
两个正交的波, 且振幅不同, 调制后相加. 得到更多的信号元素个数.
复用
一条链路传递多个信号的方法
频分复用 (FDM)
不同信号使用不同频率的载波, 叠加传输, 接收端按频率分离
时分复用 (TDM)
每个输入链接依次输出到链路上并传输. 每个输入速率相同, 且链路速率为输入数量乘以输入速率, 目的是保证输入的速率不变.
同步 TDM
每个输入 (假设有 $n$ 个输入)取一个单元 (bit / byte / block) (假设大小为 $b$), 组成一个帧. 帧大小为 $nb$. 即使某条输入此时没有数据, 也填入到帧中.
统计 TDM
帧大小小于 $nb$, 每个输入到链路上的时候, 末尾加上一个序号 (地址) 表示这个单元是谁输出的.
交换
md 第六版就没这内容
电路交换
建立
A 请求 B, B 收到后回复 A. 通过交换机建立一条通信链路.
交换机控制物理链路, 所以电路交换在物理层. 这也可以看出, 交换机 (无论是二层还是路由器) 也工作在物理层.
传输
拆除
A / B 向对方发送拆除请求, 对方不必答应. 收到请求的交换机不必在维护这条通信链路.
延迟
建立请求, 回复请求, 数据传输, 拆除请求 的 传播 和 传输 延迟. 可画时空图表示.