古典密码

代替和置换

凯撒密码

单表代替密码.

$c = p + k \mod |\Sigma|$

统计频率可以攻击

Playfair

多字母代替密码

在 $5 \times 5$ 的矩阵中, 从左到右从上到下, 先填入密钥, 然后再按顺序填入剩余字母. 其中 I = J.

明文两个字母一组. 若一组字母相同, 则插入一个字母 (如 x). 若明文长度奇数, 则最后补一个字母 (如 x).

两字母在表上

1. 同行, 用右边一个代替
2. 同列, 用下面一个代替
3. 对角线代替, (第一个字母所在行, 第二个字母所在列), (第一个字母所在列, 第二个字母所在行)

明密文不是一一对应关系, 能够降低统计规律, 但仍然有结构信息, 可被攻破.

Hill 密码

多字母代替密码

$n \times n$ 可逆矩阵 K, 明文分组, $n \times 1$ 的列向量 $p$.

加密: $c = Kp \mod |\Sigma|$

解密: $p = K^{-1}c \mod |\Sigma|$

涉及到矩阵求逆, 早不会了, 下次来补.

维吉尼亚密码

多表代替密码

对明文按密钥长度分组, 不填充. 组成 $1 \times n$ 的向量 $p$, 密钥为 $1 \times n$ 的向量 $k$.

$c = p + k \mod |\Sigma|$

最后剩余不足 $n$ 的, 组成一个向量, 密钥截断到长度相等计算.

能够显著降低统计规律, 即密文中各字母频率接近.

置换密码

一个种类的密码, 将明文进行某种置换得到密文.

轮转密码

多表代替密码

一个轮子是一种代替, 多个不同的代替依次作用在明文上, 多层加密.

分组密码

理想分组密码

长度为 $n$ 的明文空间 ($2^n$) 到长度为 $n$ 的密文空间 ($2^n$) 的一一映射, 即一个代替表, 一共 $(2^n)!$ 种一一映射.

显然密钥是映射本身. 要保存这个映射, 至少需要 $n \times 2^n$ 位, 即密钥大小为 $n \times 2^n$.

Feistel 结构

混淆confusion: 使 密文 和 密钥 之间的统计关系尽可能复杂, 常用代替 扩散diffusion: 使 密文 和 明文 之间的统计关系尽可能复杂, 常用置换

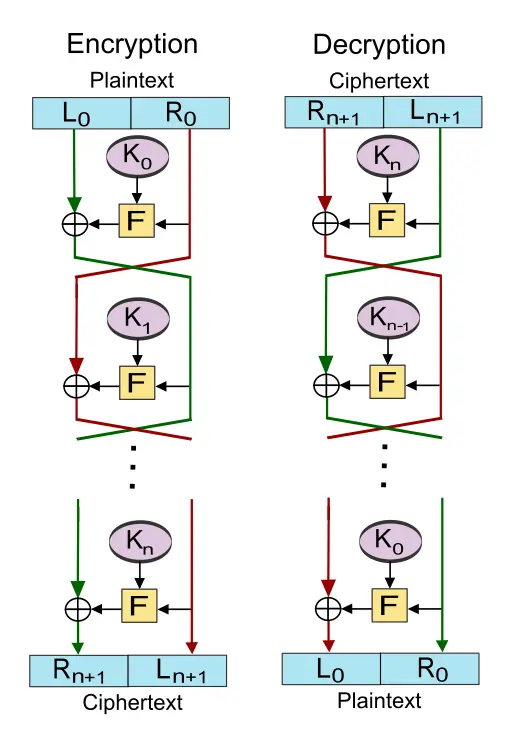
加密过程为把明文分为左右两半 L0, R0. R0 去和 K0 进行 F 操作 (加密函数), 再异或上 L0. 得到的结果作为下一轮的 R1. R0 直接作为下一轮的 L1. 即:

$$\begin{aligned} L_i & = R_{i-1} \newline R_i & = L_{i-1} \bigoplus F(R_{i-1}, K_i) \end{aligned}$$

最后一轮得到的结果为 $L_n, R_n$, 密文为 $R_n || L_n$ ($||$ 为直接连接)

根据公式, 解密为:

$$\begin{aligned} R_{i-1} & = L_i \newline L_{i-1} & = R_i \bigoplus F(R_{i-1}, K_i) = R_i \bigoplus F(L_i, K_i) \end{aligned}$$

可以发现, 加解密的结构是完全一样的. 如果密文是 $R_n || L_n$, 那么只有只有轮密钥的顺序颠倒.

需要生成轮密钥, 加密函数 F 不必可逆.

DES

https://www.ruanx.net/des/

记不住

DES 的分组为 64 位, 密钥长度为 56 位 (实际上是通过 64 位的选择). 子密钥长度 48 位.

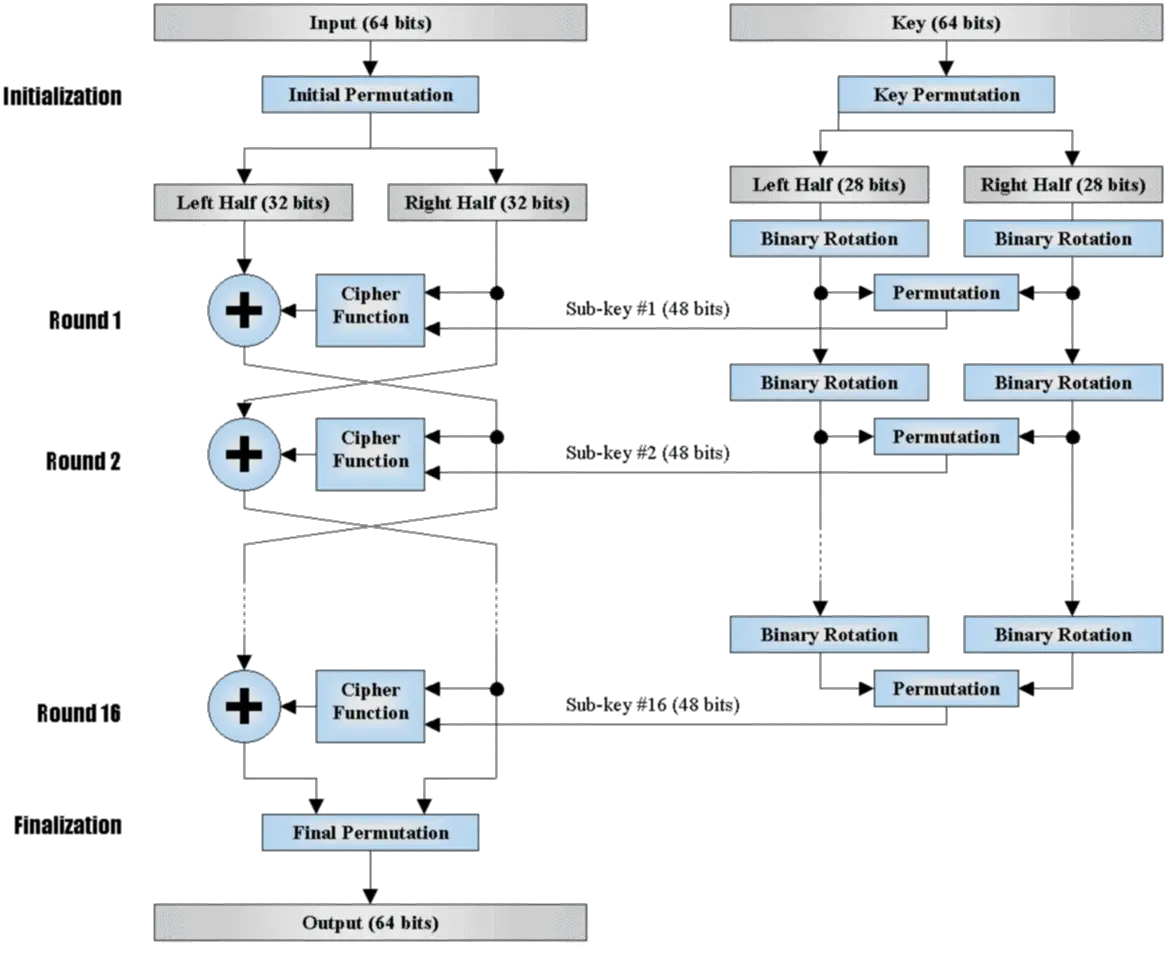
DES 是经典的 Festel 结构, 需要 子密钥, 轮函数. DES 一共进行 16 轮. 于 Festel 结构不同的地方在于, 明文在输入 Festel 网络前, 需要经过一个 IP 置换. 出网络之后经过一个 IP 逆置换 ($IP^{-1}$).

子密钥生成

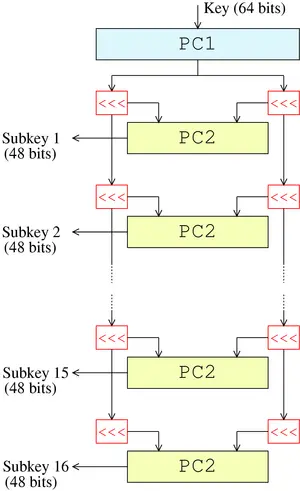
64 位的主密钥先进行一个选择置换 (PC1), 得到 48 位, 分为左右两组. 每组每轮进行一下循环左移, 然后拼接回来, 再经过一个选择置换 (PC2), 得到这一轮的子密钥. 一共进行 16 次, 得到 16 个 48 位的子密钥. 每轮的循环左移位数不尽相同, 但是是确定的. ([1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1])

轮函数

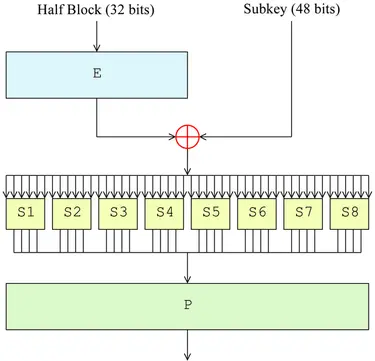
轮函数的输入是 32 位的半个明文 (或经过上一轮加密后的密文), 和 48 位的子密钥. 首先 32 位的块经过一个扩张函数 E, 得到 48 位, 与 48 位的密钥异或. 这个扩张函数实际上是一个扩张置换, 就是选择并重排这些位, 有些位在 48 个中出现不止一次.

然后将 48 位分成 8 组, 每组 6 位, 送入 8 个不同的 S 盒, 每个 S 盒输出 4 位, 组合起来一共 32 位. 最后经过一个置换 P, 输出这一轮的结果.

值得注意的是, P 是精心设计的, 使得这一轮同一个 S 盒 输出的四位, 在下一回合的扩张之后, 交由四个不同的 S 盒去处理.

雪崩效应

明文或密钥的一位变化, 将产生密文很大的差异

DES 强度

计时攻击

分析一次加解密所用时间, 分析明文或密钥的一些信息. 离最终的攻击还差很远. DES 有效抗计时攻击.

差分攻击

使用一对明文, 分析轮函数后的差分信息. DES 中 S 盒的设计有效抗差分攻击. 需要 $2^{47}$ 个选择明文 (看看就好, 不用记数字)

线性攻击

寻找加密的线性近似. DES 有效抗线性攻击. 需要 $2^{45}$ 个明文

数学基础

exgcd

妈的不会

wiki 上看到一个矩阵变换的, 非常牛逼, 简洁明了易懂.

有限域

$GF(p) = <Z_p, +_p, \times_p>$ ($p$ 是素数) 是一个有限域. 但是对任意的 $p$, 简单的 $+_p$ 和 $\times_p$ 并不构成有限域. 计算机要处理数据, 最好是 $2^n$ 这种形式. 所以要构造 $GF(2^n)$.

下面说的构造方法对 $GF(p^n)$ 都有效, 只不过 $GF(2^n)$ 比较实用, 于是只从 $GF(2^n)$ 说明.

$GF(p)$ 上的多项式 $GF(p^n)$

基于有限域 $GF(p)$, 能够构造一些多项式以及两个运算, 构造出有限域 $GF(p^n)$

我们先考虑普通多项式和普通多项式加法乘法, 他们构成一个整环, 就和整数以及普通加法乘法一样. 其中, 零元为 $0$, 幺元 (单位元) 为 $1$.

要成为一个有限域, 首先要把元素限定在有限的范围内, 然后还要求乘法除去零元构成交换群. 回想一下整数上的做法, 我们是将其模一个素数.

首先来限定元素范围.

基于有限域 $GF(p)$ 的多项式为: $$F(x) = \sum_{i=0}^{n-1} a_ix^i, (0 \le a_i < p)$$

可以发现这是一个 $n-1$ 次多项式. 同时可以看到每个系数的取值都在 $0$ 到 $p-1$ 之间, 一共有 $n$ 个, 所以这个代数系统一共有 $p^n$ 个元素. 我们想要构造的是 $GF(p^n)$

多项式加法定义为: $$\begin{aligned} F(x) + G(x) &= \sum_{i=0}^{n-1} a_ix^i + \sum_{i=0}^{n-1} b_ix^i \newline &= \sum_{i=0}^{n-1} ((a_i+b_i) \bmod p)x^i \end{aligned}$$

可以发现和普通多项式加法的区别在于系数对 $p$ 取模.

多项式乘法的定义和普通多项式乘法类似, 系数也需要对 $p$ 取模. 不过, 由于乘法会将次数提高, 从而结果不在代数集合的范围内. 于是我们需要把他 “拉” 回来.

这个方法和整数上的也类似, 就是取模. 让结果模一个多项式, 这样整个代数系统才是一个有限域.

多项式的模

假设两个多项式分别为 $3x$ 和 $4x$, $p = 7$, 那么 $3x \times 4x = (12 \bmod 7)x^2 = 5x^2$. 有 $5x^2 / 3x = 4x$ 成立. 他们两是整除关系. 和整数上的类似, 也有不能够整除, 从而多项式上有带余除法. 如 $f(x)=2x^2+3x+4$, $g(x)=3x^2+5x+2$, 有

$$f(x)/g(x)\Rightarrow f(x)=q(x)g(x)+r(x)\Rightarrow (2x^2+3x+4)=3(3x^2+5x+2)+(2x+5)$$

可以看到, $q(x) = 3$, $r(x) = 2x+5$. 他们两也是一个多项式. 还可以看到, $r(x)$ 的次数一定小于 $g(x)$ 的. 这和整数带除法类似, 余数一定小于除数.

于是, $f(x) \bmod g(x) = r(x) = 2x+5$.

那么, 想要构造把次数限定在 $n-1$, 是不是只需要模一个 $m(x) = x^n$ 呢?

多项式中的 “素数”

我们要构造的是域, 还要满足除零元外, 每个元素都有逆元这一条件. 在整数上, 我们是取质数作为模数得到的. 能否推广到多项式呢?

多项式有乘法, 有整除, 同理也有 “素数”. 它被称作 即约多项式 (不可约多项式, 素多项式).

整数上的素数也是在环上定义的, 这里我们再回到多项式环上 (实际上我们还没构造出域呢). 可以发现, 如果一个多项式, 找不到除了 $1$ 和它本身以外的因子, 那么它就是一个素多项式. 这和整数是相似的!

结合上述, 我们需要找一个 $n$ 次的素多项式, 作为模数 $m(x)$, 这样就可以将整个多项式构造成一个有限域了.

证明? 不会!

值得注意的是, exgcd 同样适用于多项式有限域 (实际上它适用于所有有限域). 所以还需要会用 exgcd 求多项式逆元.

$GF(2^n)$

在计算机中, 用的多的是像上面的方法构造出的 $GF(2^n)$ 多项式有限域. 以 $GF(2^8)$ 举例, 即:

$$F(x) = \sum_{i=0}^7 a_ix^i, (0 \le a_i < 2)$$

它的系数只能取 0 或者 1. 如果将其按照次数排列, 那么将会得到一个二进制数. 这样我们能够通过一个 8 位二进制数, 来唯一表示 $GF(2^n)$ 中的一个元素.

多项式加法用二进制表示来计算也十分简单, 系数相加然后对 2 取模, 实际上就是两个 8 位二进制数异或.

多项式乘法稍微有点复杂, 但是对于计算机来说, 是比较巧妙的. 取 $m(x)=x^8+x^4+x^3+x+1$, 假设 $f(x) = \sum a_ix^i$, 那么, $$xf(x) \bmod m(x) = \sum_{i=0}^{n-1} a_ix^{i+1} + 0$$

如果 $a_7 = 0$, 那么结果相当于系数左移, 也就是 8 位二进制数左移一位, 低位补 0.

如果 $a_7 = 1$, 那么可以看成 $x^n \bmod m(x) + \sum_{i=0}^{n-2} a_ix^{i+1}$, 只需要计算 $x^n \bmod m(x)$, $x^n \bmod m(x) = (m(x) - x^n) \bmod = x^4+x^3+x+1$. 那么也就是系数左移, 丢掉最高位, 最低位补 0, 然后异或上一个数.

如果是 $x^2f(x) \bmod m(x)$, 可以用先计算 $xf(x)$, 得到一个多项式, 然后再用相同的方法计算 $x \cdot xf(x)$, 结果也为 $xf(x)$ 左移, 然后看高位, 判断是否需要异或上一个数.

这样就得到了 $x^kf(x), (0 \le k < n)$. 对于任意多项式乘法, 都可以拆成 $\sum_{k=0}^{n-1} a_kx^kf(x), (0 \le a_k < 2)$. 根据先前得到的结果, 相加 (异或) 即可.

AES

字节替换, 行位移, 列混淆, 轮密钥加

最后一轮没有列混淆

分组密码工作模式

EBC

电密码本模式, 每组单独加密

可并行

密文异常变化只会影响到当前块

CBC

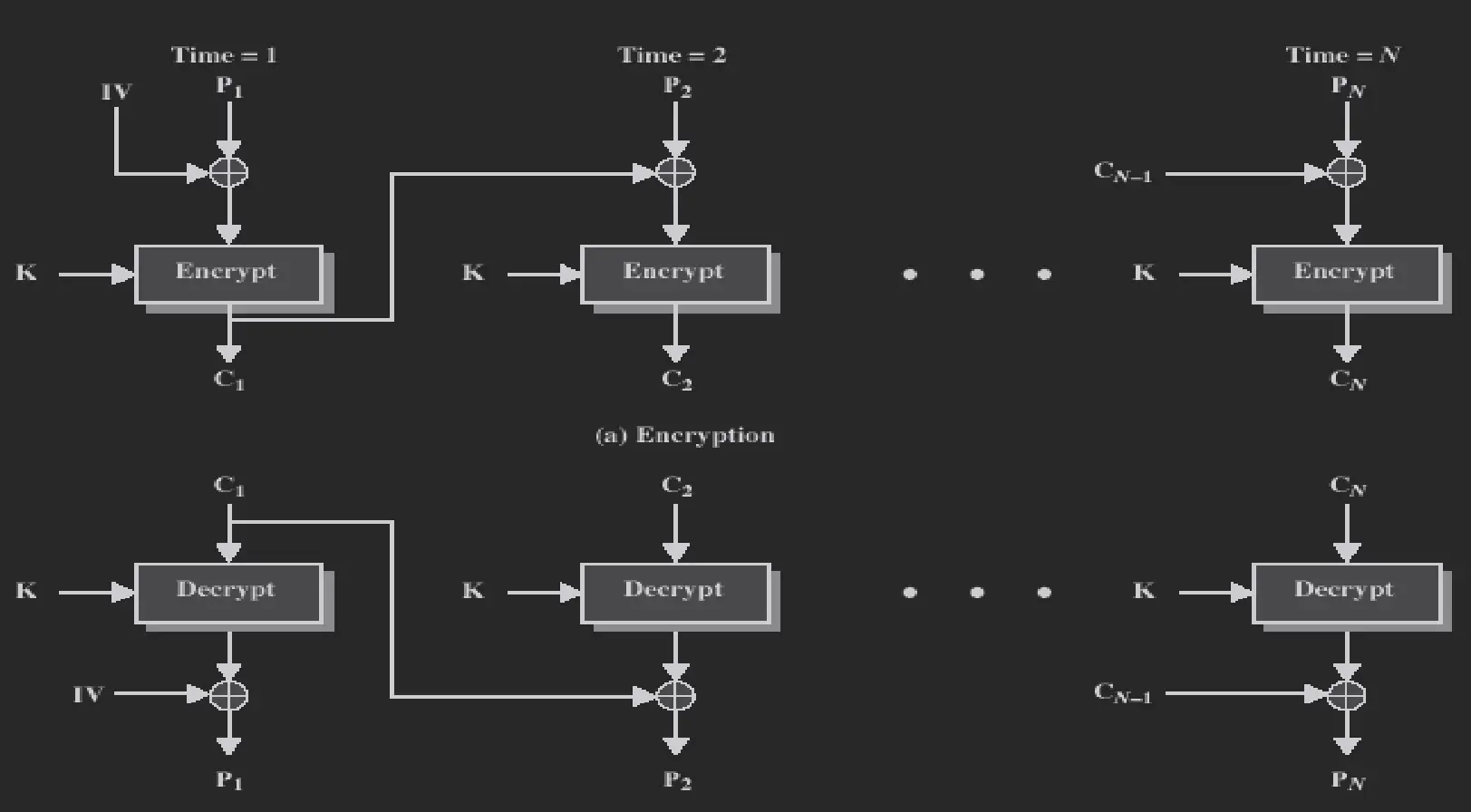
密文分组链接模式, 令 $C_0 = IV$ (初始化向量, 需指定), $C_i = E(P_i \oplus C_{i-1})$

加密不可并行, 解密可并行

密文异常变化只会影响当前块和下一块

CFB

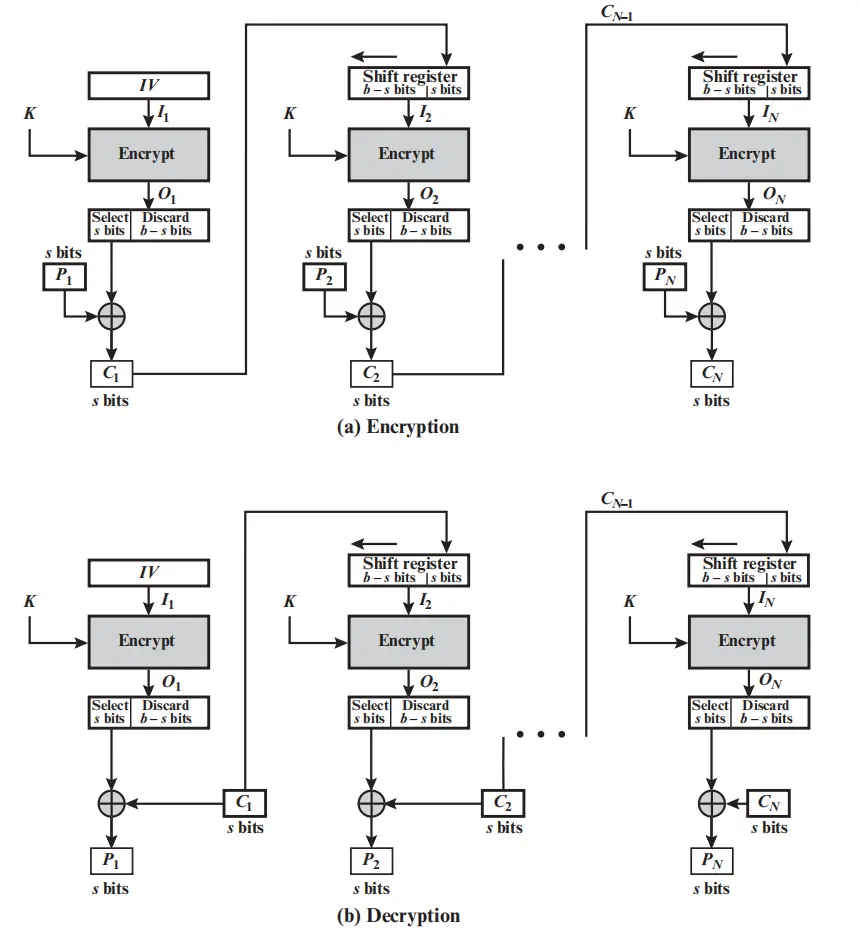
密文反馈模式. 加密分组 b 位, 明密文分组 s 位. b 位初始化向量 $IV$, 作为输入 $I_1$, 加密 $O_1 = E_K(I_1)$, 然后取 s 高位, 与 $P_1$ 异或, 得到 s 位的密文 $C_1$. 下一个输入 $I_i = I_{i-1} « s | C_{i-1}$, 继续操作.

当 s = 8 时, 可以一个一个字节加密, 相当于流密码

加解密都使用加密运算

加密不可并行, 解密可并行

密文异常变化影响从当前块开始的 $\lceil\frac{b}{s}\rceil$ 组

OFB

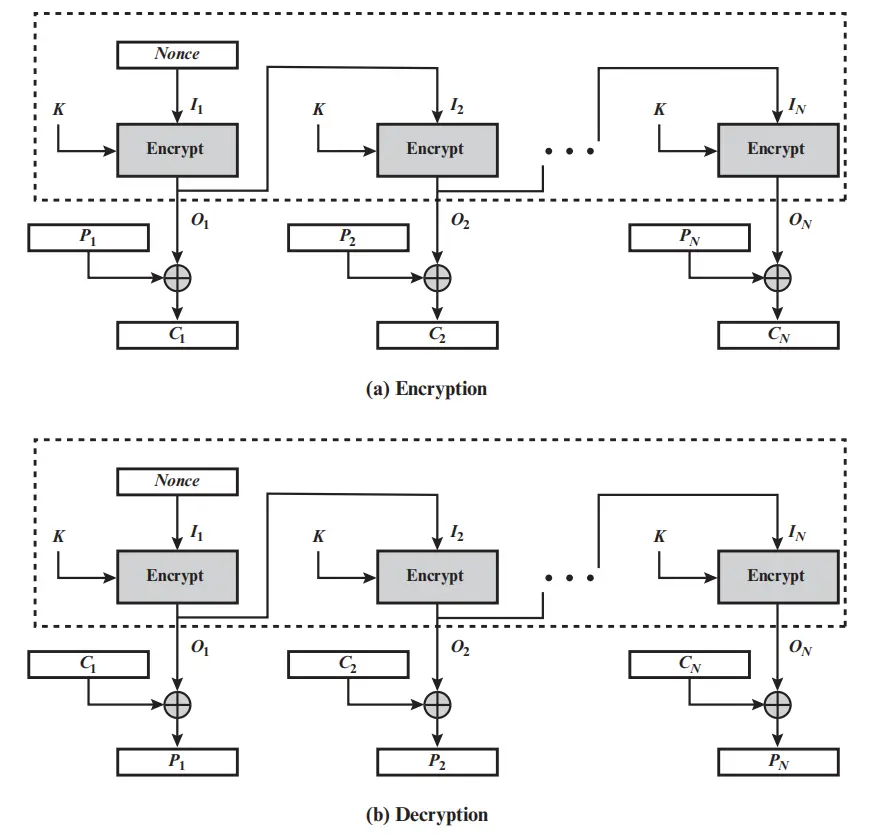
输出反馈模式, 加密分组 b 位, 明密文分组 s 位. 看图就行. 加密输出取高 s 位与明文或密文进行异或

密文异常变化只会影响当前组

CTR

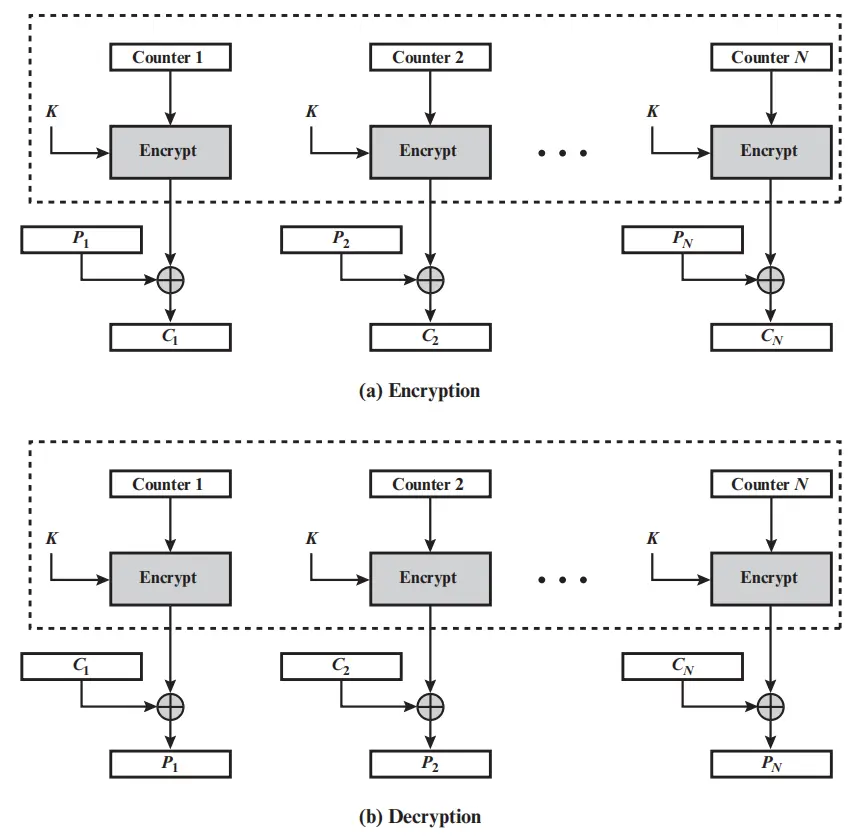
计数器模式, 加密分组 b 位, 明密文分组 s 位. $T1$ 取随机值, 之后 +1. 看图即可. 加密输出取高 s 位与明文或密文异或

加解密可并行, 随机访问, 只用到加密算法, 密文异常变化只会影响当前分组.

随机数

应用:

• 临时交互信号, 防止重放攻击
• 密钥产生

伪随机数发生器指标:

• 均匀性: 0 和 1 出现的大致概率相等
• 可伸缩性: 任何子序列都要通过随机性测试
• 一致性: 对所有种子, 产生的序列都要通过随机性测试

随机性测试:

• 频率测试: 0 和 1 数目是否大致相等
• 游程测试: 各种长度的 0 或者 1 游程数目是否像真随机序列期望的一样 (游程: 序列中连续相同的子段)
• Maurer通用测试: 能否被明显压缩, 不能被压缩说明随机性好

不可预测性:

• 前向不可预测: 不知道种子无法推测序列的下一位
• 后向不可预测: 知道序列无法推测种子

不可重现性: 除非保存, 否则无法重现序列

伪随机数分类:

• 弱伪随机数: 满足随机性
• 强伪随机数: 满足随机性, 不可预测性
• 真随机数

分类:

• 伪随机: 看起来随机, 能通过许多随机性测试
  • 弱伪随机: 满足随机性
  • 强伪随机: 满足随机性, 不可预测性
• 真随机: 满足随机性, 不可预测性, 不可重现性

密码学意义的随机至少为强伪随机

伪随机数发生器

线性同余发生器

$$x_{n+1} = (ax_n + c) \bmod m$$

输出的序列取决于参数的选择.

1. $gcd(a, m) = 1$
2. $m$ 为素数, $c = 0$, 则序列周期为 $m-1$
3. 可取 $m$ 为梅森素数 $2^n - 1$, 即 $x_{n+1} = ax_n \bmod m$

准则:

• 完整周期: $0$ - $m-1$ 都要出现
• 满足随机性测试
• 可高效实现

优点: 方便快速

缺点: 由确定算法产生, 可被破译

密码学不能使用, 但是其他应用广泛

BBS 发生器

1. 选择两个大素数 $p, q$, 满足 $p \equiv q \equiv 3 \mod 4$
2. $n = pq$
3. 选择 $x_{-1}$, 满足 $gcd(x_{-1}, n) = 1$
4. $x_i = x_{i-1}^2 \bmod n$
5. $B_i = x_i \bmod 2$

优点: 密码学意义安全

缺点: 计算量大

对称加密产生随机数

• 循环加密: $$x_i = E_K(i)$$
• DES OFB 加密
• ANSI X9.17: 三重DES (EDE), $R_i = EDE(v_i \oplus EDE(DT_i)), v_{i+1} = EDE(R_i \oplus EDE(DT_i))$, $DT_i$ 为时间, $v_0$ 为种子

RC4 流密码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

key = b'key'
S = list(range(256))
T = (key * 256)[:256]

j = 0
for i in range(256):
    j = (j + S[i] + T[i]) % 256
    S[i], S[j] = S[j], S[i]

i = j = 0
ciphertext = ''
for p in plaintext:
    i = (i + 1) % 256
    j = (j + S[i]) % 256
    S[i], S[j] = S[j], S[i]
    t = (S[i] + S[j]) % 256
    k = S[t]
    print(k)
    ciphertext += chr(p ^ k)

记 nm 呢

避免重复使用密钥, 否则会被破译

抗线性攻击和差分攻击

密钥长度可变

快

加解密算法相同

数论基础

费马小

$a^{p-1} \equiv 1 \mod p$

欧拉定理

$\phi(x)$ 为小于 $x$ 且与 $x$ 互质的整整数个数

• $\phi(1) = 1$
• $\phi(p) = p-1$
• $\phi(2^k) = 2^{k-1}$
• $\phi(pq) = \phi(p)\phi(q) = (p-1)(q-1)$
• $\phi(\prod_{i=1}^n p_i^{e_i}) = \prod_{i=1}^n p_i^{e_i-1}(p_i-1)$

$(a, n) = 1$ 时, $a^{\phi(n)} = 1 \mod n$

Miller-Rabin

检测奇数 p 是否为素数. $p - 1$ 为偶数, 那么就能够写成 $p - 1 = 2^rd$ 的形式. 如果 $p$ 是素数, 由费马小得, $a^{p-1} \equiv 1 \mod p$, 即 $(a^d)^{2^r} \eqiuv 1 \mod p$, 这样开根, 如果 $p$ 是素数, 那么根只会是 $1$ 或者 $-1$ ($p-1$).

也就是说, 对于 $a^d, a^2d, a^{2^2}d, \dots, a^{2^r}d$ 这个序列, 要么全是 $1$, 要么从某个地方开始是 $-1$, 之后全是 $1$. 这样 $p$ 才可能是素数, 否则一定不是素数.

多找几个 $a$, 多测试, 就可以在错误率很低的情况下判定素数.

CRT

解线性同余方程组

$$\begin{cases} x \equiv a_1 \mod m_1 \newline x \equiv a_2 \mod m_2 \newline \dots \newline x \equiv a_n \mod m_n \end{cases}$$

其中, $m_i$ 两两互质

1. $M = \prod m_i$, $M_i = \frac M {m_i}$
2. 求 $M_i$ 在 模 $m_i$ 下 的逆元 $M_i^{-1}$
3. $x = \sum M_iM_i^{-1}a_i \mod M$

离散对数

求最小的 $x$, 使得 $a^x \equiv b \mod m$, 其中 $m > 1, gcd(a, m) = 1$

若 $m$ 是素数 $p$, 且 $a^i \bmod p$ 各不相同, 则 $a$ 是 $p$ 的原根

此时一定有解, 可表示为 $x = d\log_{a, p} (b)$

$(a, m) = 1$, $a$ 模 $m$ 的阶为 $\phi(m)$, 则称 $a$ 是模 $m$ 的原根. (阶就是循环群那个阶的意思)

公钥密码

对称密码的缺点:

• 密钥量大, 难管理
• 无法实现签名, 认证等

基本原理: 加解密使用不同的密钥, $E_k$, $D_k$ 有联系, 但是不能相互推导

优点: 对称密码的缺点反一下

安全性: 基于计算复杂度理论

• 单向函数: $\forall x \in D$, $f(x)$ 容易计算. $\forall y \in V$, $f^{-1}(y)$ 难以计算
• 单向陷门函数: 已知某些秘密信息, 求逆简单

背包密码

01 背包问题

超递增背包: 第 $i$ 个物品重量大于之前的总和. 超递增背包问题容易解决, 从大到小考虑物品, 比剩余容积小就放

不看了

RSA

1. 选择大素数 $p, q$, $p \ne q$
2. $n = pq, \phi(n) = (p - 1)(q - 1)$
3. 选择 $e$, $1 < e < \phi(n)$, $gcd(e, \phi(n)) = 1$
4. 计算 $d = e^{-1} \mod \phi(n)$
5. 公钥: $(e, n)$, 私钥: $(d, n)$

加密: $c = m^e \bmod n$, 解密 $m = c^d \bmod n$

攻击方法:

• 枚举 $d$
• 分解 $n$
• 计时攻击: 一种侧信道, 观察加密所用时间来猜测密钥
• 小指数攻击: 不知道是什么

参数选择:

跳过

DH 密钥交换

基于离散对数问题

素数 $p$, 以及模 $p$ 的原根 $g$ 公开, Alice 和 Bob 各自保存一个数 a (b)

sequenceDiagram
    participant Alice
    participant Bob

    Alice->>Bob: 发送公开参数 (p, g)
    Bob->>Alice: 接收公开参数 (p, g)
    Alice->>Bob: 发送 A = g^a mod p
    Bob->>Alice: 发送 B = g^b mod p
    Alice->>Bob: 计算密钥 K = B^a mod p
    Bob->>Alice: 计算密钥 K = A^b mod p

中间人攻击:

DH 交换中没有提供密钥的认证功能, 所以可以被中间人攻击

sequenceDiagram
    participant Alice
    participant Eve
    participant Bob

    Alice->>Bob: 发送公开参数 (p, g)
    Note left of Eve: 截获 (p, g)
    Bob->>Alice: 接收公开参数 (p, g)
    Alice->>Eve: 发送 A = g^a mod p
    Bob->>Eve: 发送 B = g^b mod p
    Eve->>Alice: 发送伪造的 B' = g^b' mod p
    Eve->>Bob: 发送伪造的 A' = g^a' mod p
    Alice->>Eve: 计算密钥 Ka = B'^a mod p = g^ab' mod p
    Eve->>Alice: 计算密钥 Ka = A^b' mod p = g^ab' mod p
    Note left of Eve: 与 Alice 通信使用密钥 Ka
    Bob->>Eve: 计算密钥 Kb = A'^b mod p = g^a'b mod p
    Eve->>Bob: 计算密钥 Kb = B^a' mod p = g^a'b mod p
    Note right of Eve: 与 Bob 通信使用密钥 Kb

ElGamal 密码

基于离散对数问题

公开 (p, g), 随机整数 x

加密:

1. 选择随机整数 k, $(k, p-1) = 1$
2. $c = (c_1, c_2) \equiv (g^k, mg^{kx})$

解密:

$c_2(c_1^x)^{-1} \equiv mg^{kx}(g^{kx})^{-1} \equiv m$

特点:

• 明文消息均匀分布到密文空间中
• 对不同消息要选择不同随机数 k, 否则会被攻破
• 缺点: 需要随机数, 密文长度加倍

哈希函数

用途: 消息认证码, 数字签名前的预处理等

要求:

1. 任意长度输入, 固定长度输出
2. 无法求逆
3. 很难找到给定原文的碰撞
4. 很难找到一对碰撞

• 单向哈希函数满足 1 - 2
• 弱哈希函数满足 1 - 3
• 强哈希函数满足 1 - 4

生日攻击

生成很多原文, 找碰撞, 两个哈希值相同的概率很大

消息认证

• 哈希:
  • 发送 $E_K(M || H(M))$
  • 发送 $M || E_K(H(M))$
  • 发送 $M || H(M || S)$ ($S$ 是盐值)
  • 发送 $E_K(M || H(M || S))$
• 加密
  • 对称密码: 明文要可以识别, 或者含有冗余的校验
  • 公钥: 私钥签名
• 消息认证码 (MAC)

MAC

$MAC = C_K(M)$, 但不要求 $C$ 可逆. $C$ 公开, 产生固定长度的密文 (有点像带有密钥的哈希函数), $K$ 共享

有对称密码为什么需要 MAC

• 某些情况只需要认证 (广播)
• 将认证和加密分开, 使系统设计的层次更灵活
• 解密后的持续保护

MAC 函数的要求和哈希类似

1. 均匀扩散
2. 难碰撞
3. 依赖原文的所有比特位

HMAC

$K^+$ 是密钥 $K$ 左边填充 0 到 b bit

$HMAC = H[(K^+ \oplus opad) || H[(K^+ \oplus ipad) || M)]]$

应该也不考细节实现什么的

数字签名

消息认证可以保护信息不被第三方攻击, 防伪装, 修改(内容, 顺序, 计时等)

数字签名保证消息不可抵赖 (双方可能发送自身的攻击), 防发送方否认, 接收方否认

直接数字签名: 用自己的私钥签名, 先签名后加密, 缺点是安全性依赖于发送方私钥的安全性

仲裁数字签名: 第三方, 加时间

RSA, ElGamal

密钥管理与分发

对称密钥分发

基于 KDC 的密钥分发

KDC 有用户的主密钥 (KA, KB), 仅 KDC 和对应终端知道, KDC 用于分配 AB 通信的会话密钥 KAB

sequenceDiagram
    participant A
    participant KDC
    participant B

    A->>KDC: IDA || IDB || N1
    KDC->>A: E(KA, KAB || [IDA || IDB || N1] || E(KB, IDA, KAB))
    A->>B: E(KB, IDA || KAB)
    B->>A: E(KAB, N2)
    A->>B: E(KAB, f(N2))

其中, N1 是此次传输的唯一标志, 称为临时交互号, 可以是时间戳, 计数器, 随机数. 每次不同.

KDC 向 A 发回先前的请求, A 就知道是否被修改或者重放 (同一个 N1 收到多次那就是被重放了)

B 发送的 N2 也是临时交互号, 用于防止重放攻击

• 对有链接的协议 (如 TCP), 每个会话链接用不同的密钥
• 对无链接的协议, 定期更改会话密钥

公钥加密的密钥分发

sequenceDiagram
    participant A
    participant B

    A->>B: E(PUb, N1 || IDA)
    B->>A: E(PUa, N1 || N2)
    A->>B: E(PUb, N2)
    A->>B: E(PUb, E(PRa, Ks))

公钥分发

1. 公开发布: 可能被伪装
2. 公开可访问目录: 目录可行, 包含 (姓名, 公钥) 对. 可能被篡改
3. 公钥授权: 公开可访问目录 + 授权访问
4. 公钥证书: 可行第三方发证书, 通过证书认证

公钥授权

公钥授权中心的公钥 PUauth 公开, 供终端收到消息后验证

sequenceDiagram
    participant A
    participant Auth
    participant B

    A->>Auth: request || Time1
    Auth->>A: E(PRauth, PUb || request || Time1)
    A->>B: E(PUb, IDA || N1)
    B->>Auth: request || Time2
    Auth->>B: E(PRauth, PUa || request || Time2)
    B->>A: E(PUa, N1 || N2)
    A->>B: E(PUb, N2)

(request 可以为 IDA || IDB, 和前面的一样)

公钥证书

sequenceDiagram
    participant A
    participant CA
    participant B

    A->>CA: PUa
    CA->>A: Ca = E(PRca, Time1 || IDA || PUa)
    B->>CA: PUb
    CA->>B: Cb = E(PRca, Time2 || IDB || PUb)
    A->>B: Ca
    B->>A: Cb

X.509 认证服务

证书格式:

CA«A» = CA{V, SN, AI, CA, TA, A, Ap}

• Y«X»: Y 颁发给 X 的证书
• Y{I}: Y 签名 I, 即 I || H(E(PRcz, I))
• V: 版本
• SN: 序列号
• AI: 签名算法标识
• CA: 证书签署机构名称
• TA: 有效期
• A: A 名称
• Ap: PUa

CA 层次

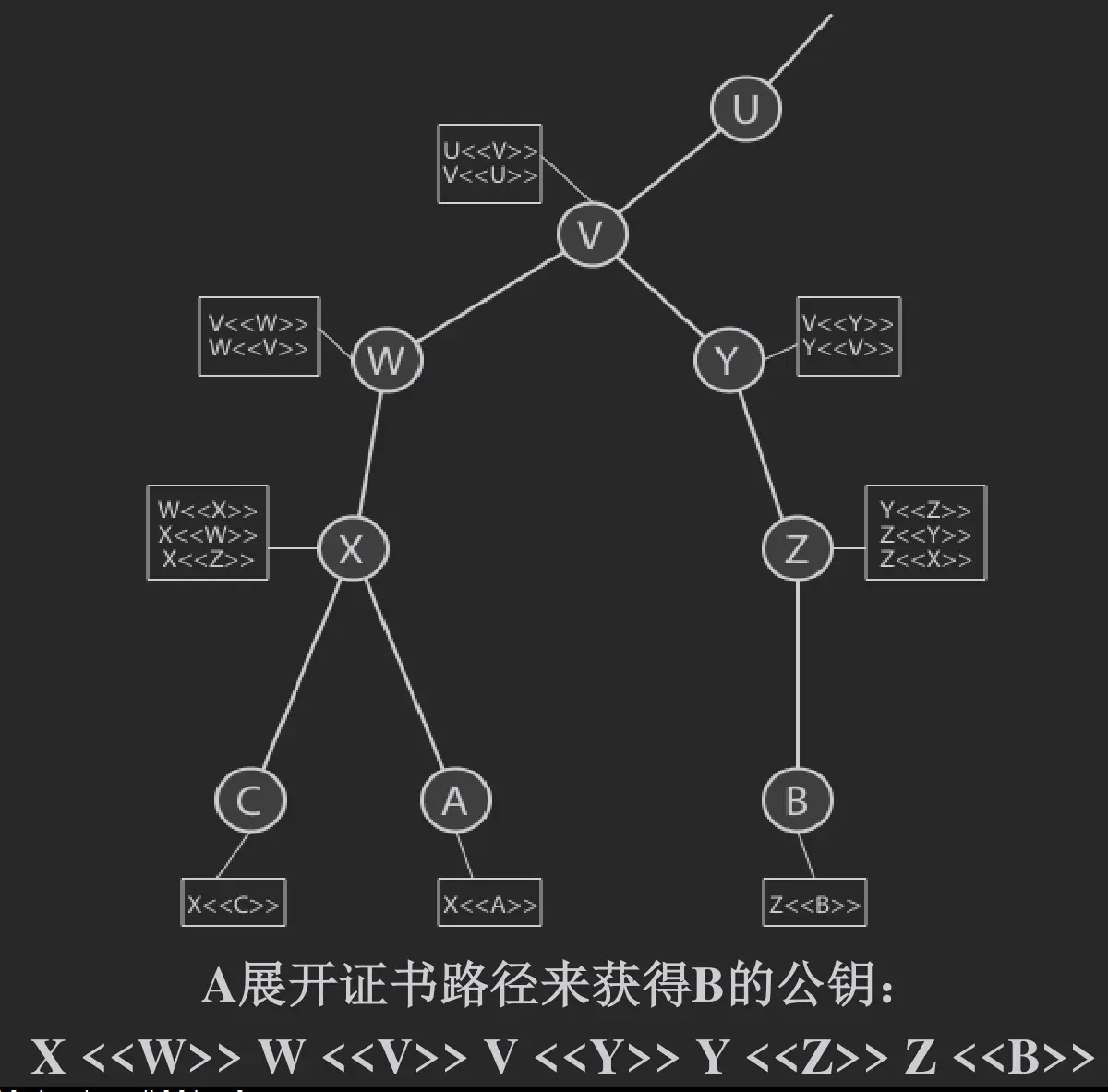
相邻的 CA 需要相互颁发证书.

A 不断从目录中找, 不是 CA 替他找

公钥基础设施

PKI系统是有硬件、软件、人、策略和程序构成的一整套体系

• 端实体
• 签证机构CA
• 注册机构RA
• 证书撤销列表发布CRL
• 证书存储库

用户认证

Needham-Schroeder 协议

sequenceDiagram
    participant A
    participant KDC
    participant B

    A->>KDC: IDA || IDB || N1
    KDC->>A: E(KA, KAB || [IDA || IDB || N1] || E(KB, IDA, KAB))
    A->>B: E(KB, IDA || KAB)
    B->>A: E(KAB, N2)
    A->>B: E(KAB, f(N2))

就是上面这个玩意, 后面 A, B 通信的过程就是相互认证的过程

添加时间戳抗重放攻击

A B 不同时在线需要单向认证, 去除最后两步, 然后 A 直接用会话密钥加密信息发送给 B. 不能抗重放攻击.

Kerberos

看不明白细节, 搞清楚 AS, TGS, TGT 和大致过程应该够了吧qaq

优点:

• 分布式, 能在不安全的信道中安全通信
• 无法伪造服务票据获得未授权服务
• 能够防止重放攻击 (重放服务操作)
• 对称加密, 高效

公钥加密方法认证

双向认证 Denning 81 协议:

sequenceDiagram
    participant A
    participant AS
    participant B

    A->>AS: IDA || IDB
    AS->>A: E(PRas, IDA || PUa || T) || E(PRas, IDB || PUb || T)
    A->>B: E(PRas, IDA || PUa || T) || E(PRas, IDB || PUb || T) || E(PUb, E(PRa(M | T)))

单向:

最后一步改变, 若

1. 关心保密: E(PUb, Ks) || E(Ks, M)
2. 关心签名: M || E(PRa, H(M)) || E(PRas, IDA || PUa || T) (相当于是消息 + 签名摘要 + 证书)

SSL

记录协议

(了解一下)

建立在可靠传输协议之上, 提高保密性和完整性

分割数据流, 每段单独保护传输

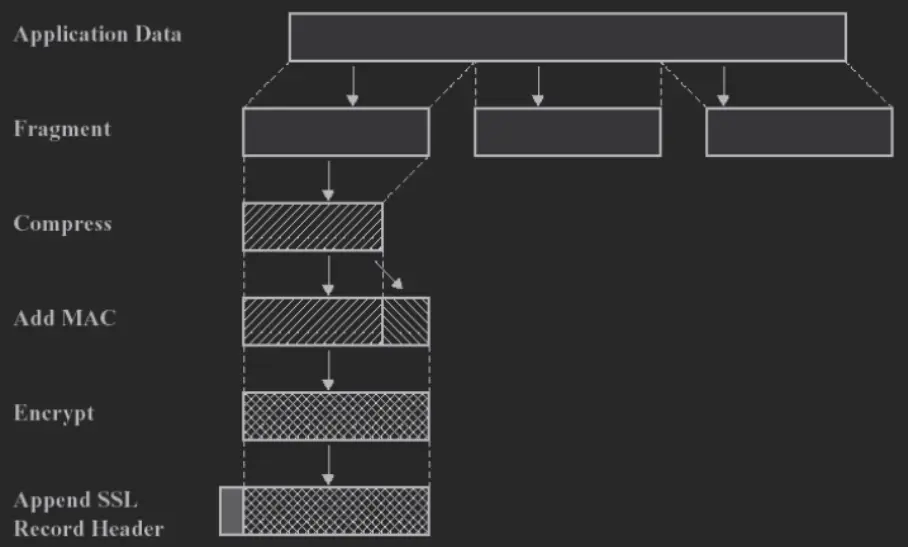
payload 可为修改密码规范协议, 报警协议, 握手协议, 上层协议

握手协议

目的:

• 协商加密算法
• 确定加密密钥
• 对客户端进行认证 (可选)

sequenceDiagram
  participant Client
  participant Server

  Client->>Server: client_hello
  Server->>Client: server_hello
  Server->>Client: certificate
  Server->>Client: server_key_exchange
  Server->>Client: certificate_request
  Server->>Client: server_hello_done
  Client->>Server: certificate
  Client->>Server: client_key_exchange
  Client->>Server: certificate_verify
  Client->>Server: change_cipher_spec
  Client->>Server: finished
  Server->>Client: change_cipher_spec
  Server->>Client: finished

阶段一: 建立安全功能

• client_hello: SSL 版本, 随机数, 会话标志 (新的会话还是已有会话创建新的链接), 支持的密码套件, 支持的压缩方法.
• server_hello: 相同, SSL 版本范围是客户端支持的最低版本到服务器支持的最高版本. 密码套件和压缩方法是从客户端支持的选出来的.

密码套件包含密钥交换方法, 密码算法, MAC 算法, 密码类型 (流/块), HASH 方法等.

密钥交换方法 (如何交换会话密钥):

• RSA: 用接收者的公钥加密会话密钥, 服务器要发公钥证书
• 固定 DH: 证书中包含 DH 公钥
• 瞬时 DH: 用发送者的 RSA 私钥签名临时的 DH 公钥
• 匿名 DH: 不认证, 直接发 DH 公钥

阶段二: 服务器认证和密钥交换

• certificate: 服务器发证书 (匿名 DH 方法不需要)
• server_key_exchange: 服务器发送密钥交换方法必要的参数 (固定 DH 因为证书中包含了公钥所以不需要这个, RSA 也不需要)
• certificate_request: 服务器发送, 请求客户的证书 (匿名 DH 不需要, 其他都需要)
• server_hello_done: 结束, 等待应答

阶段三: 客户端认证和密钥交换

客户端检查 server_hello 参数是否能用, 认证服务端.

• certificate: 客户端发送证书 (如果有请求)
• client_key_exchange: 客户端根据密钥交换方法, 发送不同内容
  • RSA: 客户端生成的次密钥
  • 瞬时/匿名 DH: DH 公钥
  • 固定 DH: 证书包含了, 所以这个包为空
• certificate_verify: 用私钥签名握手消息的 MAC (可选)

阶段四: 完成

• change_cipher_spec: 客户端使用修改密码协议发送, 修改密码. 客户端把协商的密码规范复制到当前链接状态中 (就是换密码)
• finished: 客户端发送用新密码规范加密握手消息的 MAC

服务器同样发送 change_cipher_spec 和 finished

IPSec

在网络层对 IP 包进行加密, 认证

IPSec 可以提供:

• 访问控制
• 无连接完整性 (UDP 数据包完整)
• 数据源认证
• 加密
• 防重放

AH 和 ESP

• AH: 认证头, 认证整个 IP 包
• ESP: 封装安全性有效载荷, 提供 IP 报文的保密性, 可选提供报文认证 (不认证 IP 头)

模式

• 传输模式: 直接加头或 (和) 尾, 不改变 IP 头
• 隧道模式: 封装整个 IP 包为另一个 IP 包

封装

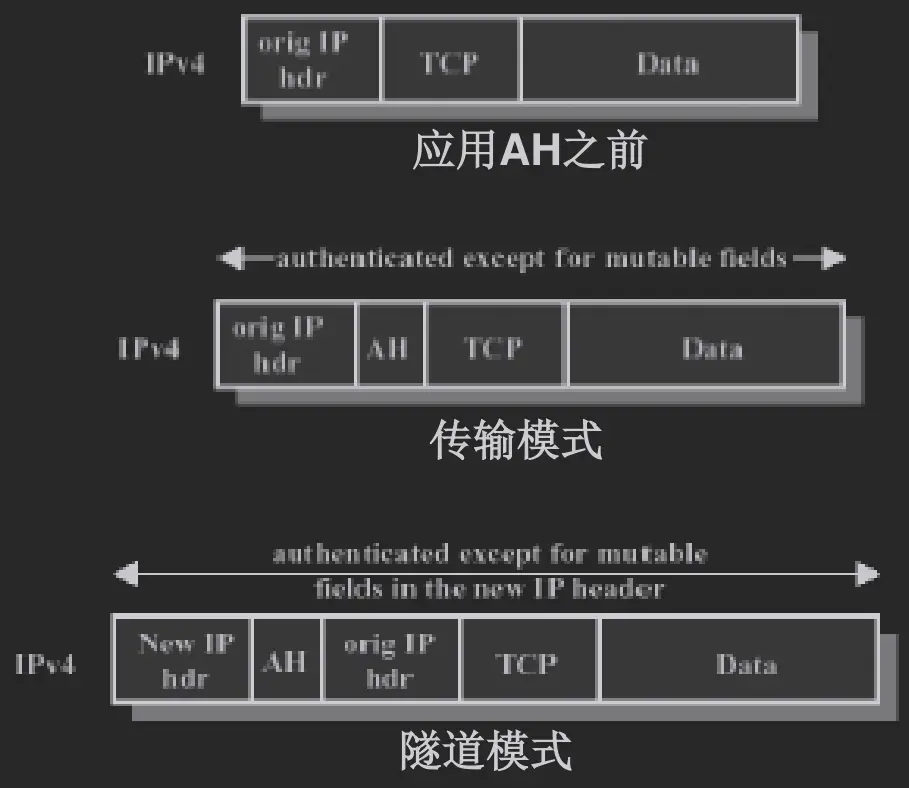
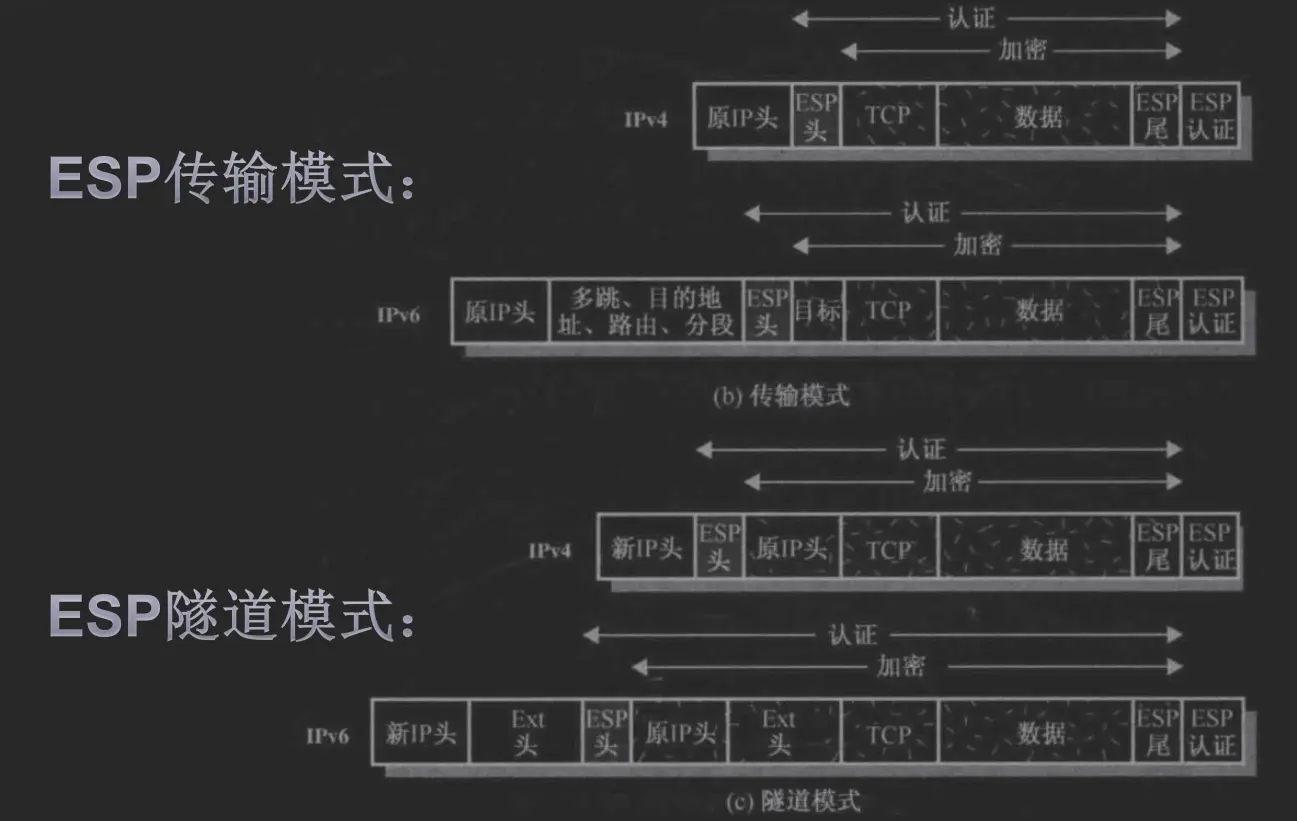
ESP 认证 + 加密

1. ESP 自己的认证功能
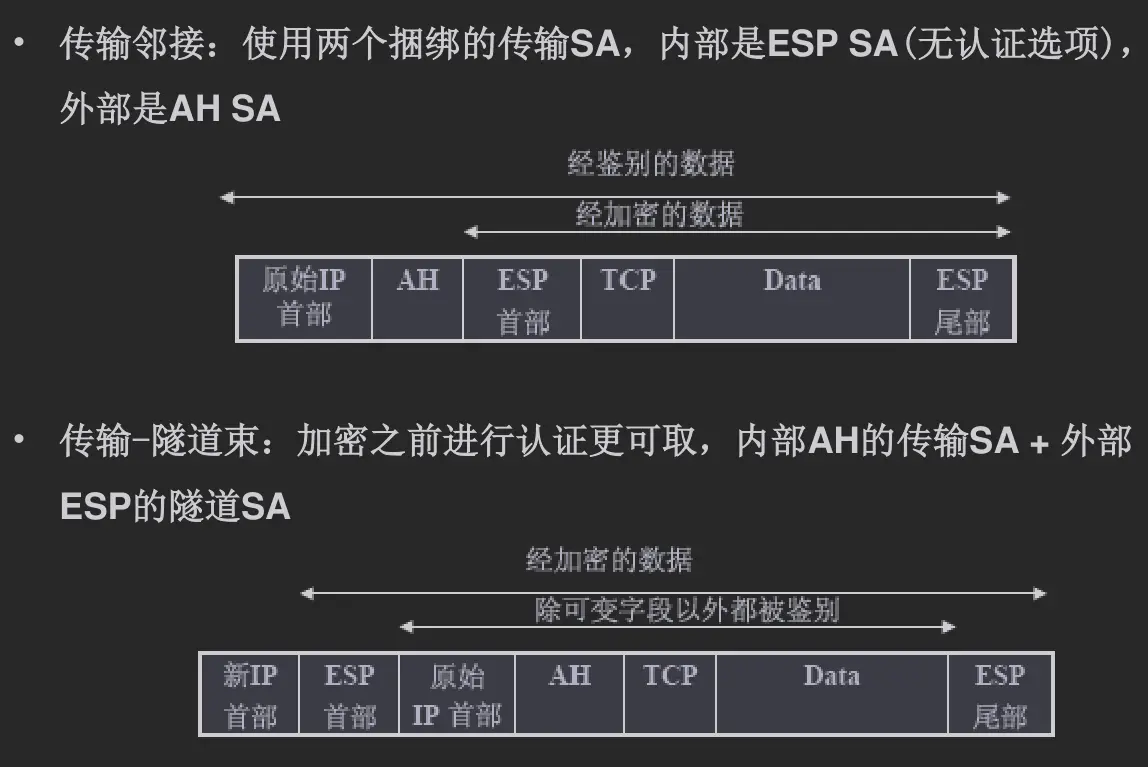
2. 传输邻接: 先传输 ESP 加密, 再传输 AH 认证
3. 传输-隧道束: 先传输 AH 认证, 再隧道 ESP 加密