「笔记」人工智能导论

Wings 收录于类别期末速通

2023-06-14 2023-06-14 约 1202 字预计阅读 6 分钟次阅读条评论

第一章绪论

(大概不用看绪论了)

定义

用人工的方法在计算机上实现的智能

发展

孕育阶段: 各种逻辑学, 计算机学的发展
形成阶段: 提出人工智能, 并有所研究
发展阶段: 各种专家系统, 到今天的东西

研究内容

机器感知: 模式识别, 自然语言理解与机器翻译
机器思维:
- 知识表示
- 知识管理
- 知识推理
- 启发式搜索
- 神经网络, 人脑结构
机器学习
机器行为: 机器人
智能系统及其构造技术

研究途径

生物学观点: 科学的观点, 研究人类智能的本质, 神经网络
认知学观点: 工程的观点, 运用计算机科学, 模拟智能, 符号处理

派别

符号主义: 认为人工智能起源于数理逻辑, 基于物理符号系统假设和有限合理性原理, 以知识的符号表达为基础, 利用推理进行问题求解
连接主义: 认为人工智能来源于仿生学, 基于神经网络及其间的连接机制和学习算法, 以人工神经网络为代表
行为主义: 认为人工智能起源于控制论, 智能取决于感知和行为, 取决于对外界复杂环境的适应, 而不是表示和推理

人工智能学术派别之争趋于平和, 走向集成和合作

传统三大核心研究内容

知识表示
知识推理
知识应用

应用

问题求解
机器学习
自然语言
专家系统
模式识别
计算机视觉
机器人学
博弈
计算智能
人工生命
自动证明
自动程序设计
智能控制
智能检索
智能调度与指挥
智能决策
神经网络
数据挖掘

知识表示

数据: 信息的载体和表示
信息: 数据的语义
知识: 有关信息联系在一起形成的信息结构

特性:

相对正确性
不确定性
可表示可利用

知识表示是计算机可接收的用于描述知识的数据结构, 即对知识的描述

符号表示法
连接机制法: 神经网络

状态空间

略

问题归约

将大问题分解成小问题, 小问题与或逻辑组合成大问题

本原问题: 不能再分解且直接可解的问题

可构造树 (解树, 与或树)

谓词逻辑

暂时略, 离散忘记光了

语义网络

(好像不是重点)

带标识的有向图

节点表示

表示概念:

有属性, 可继承 (箭头继承于)

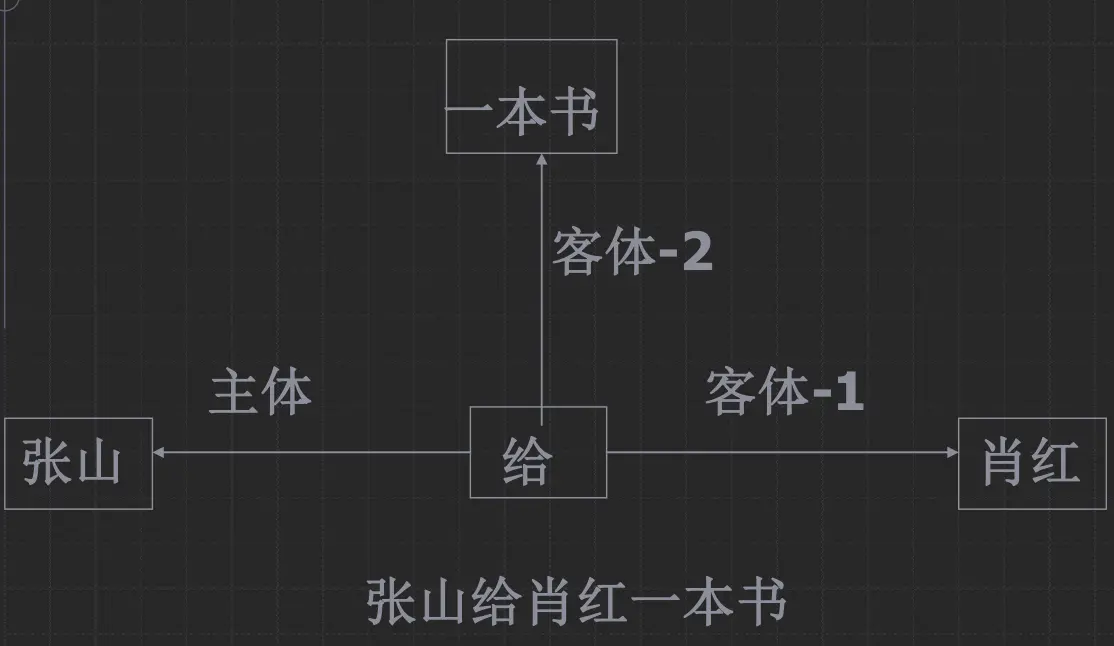
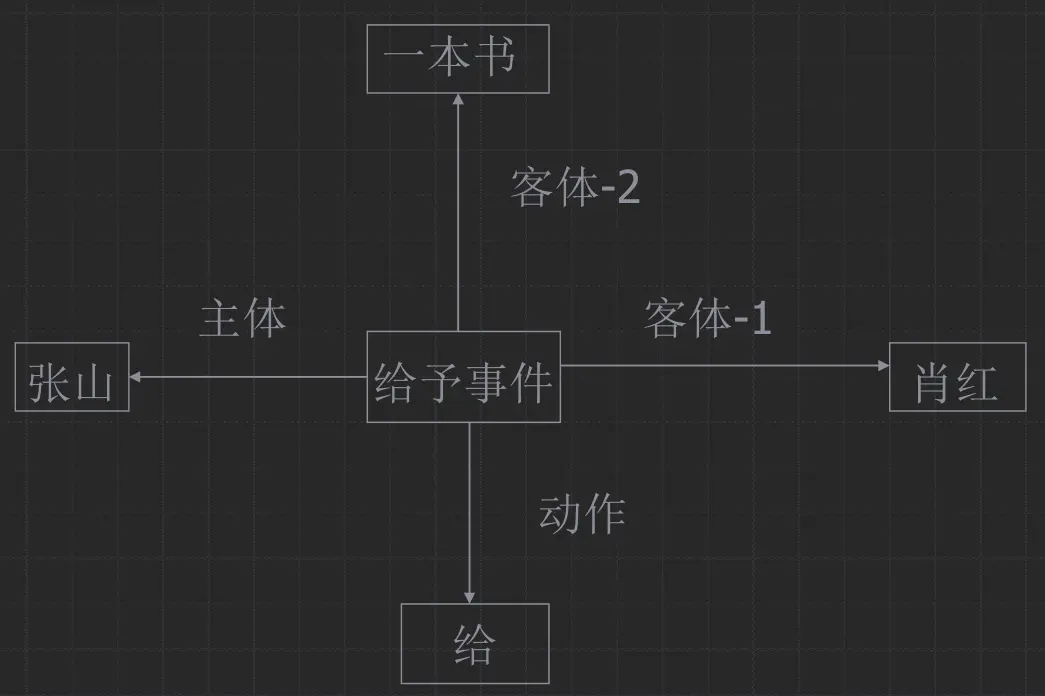
语义网络表示

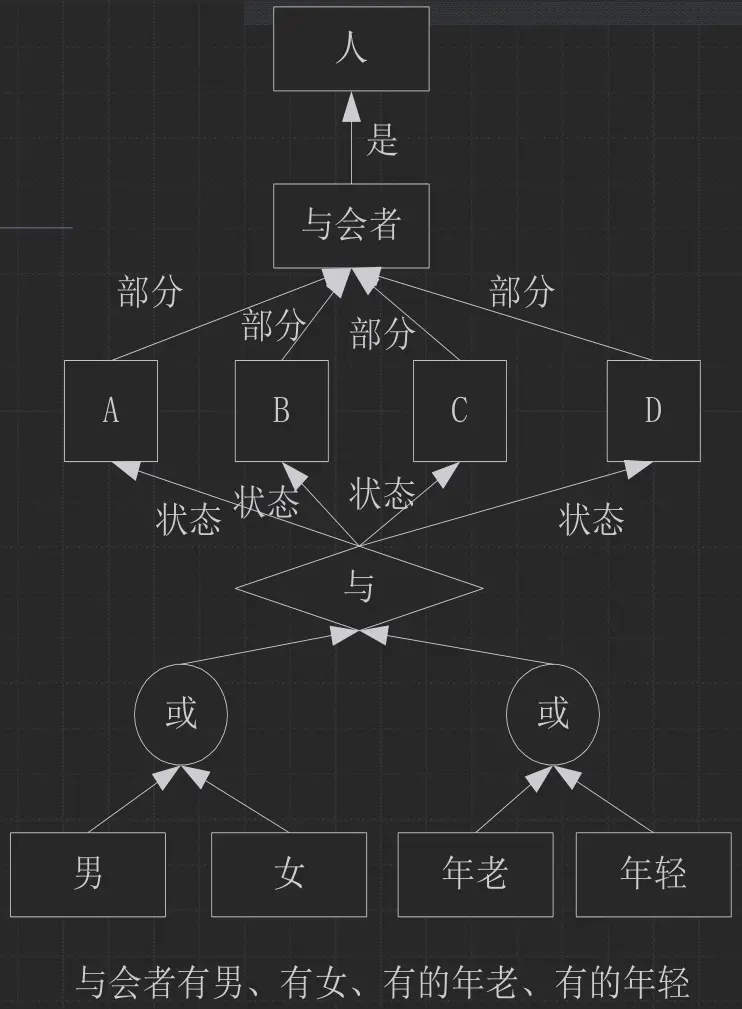
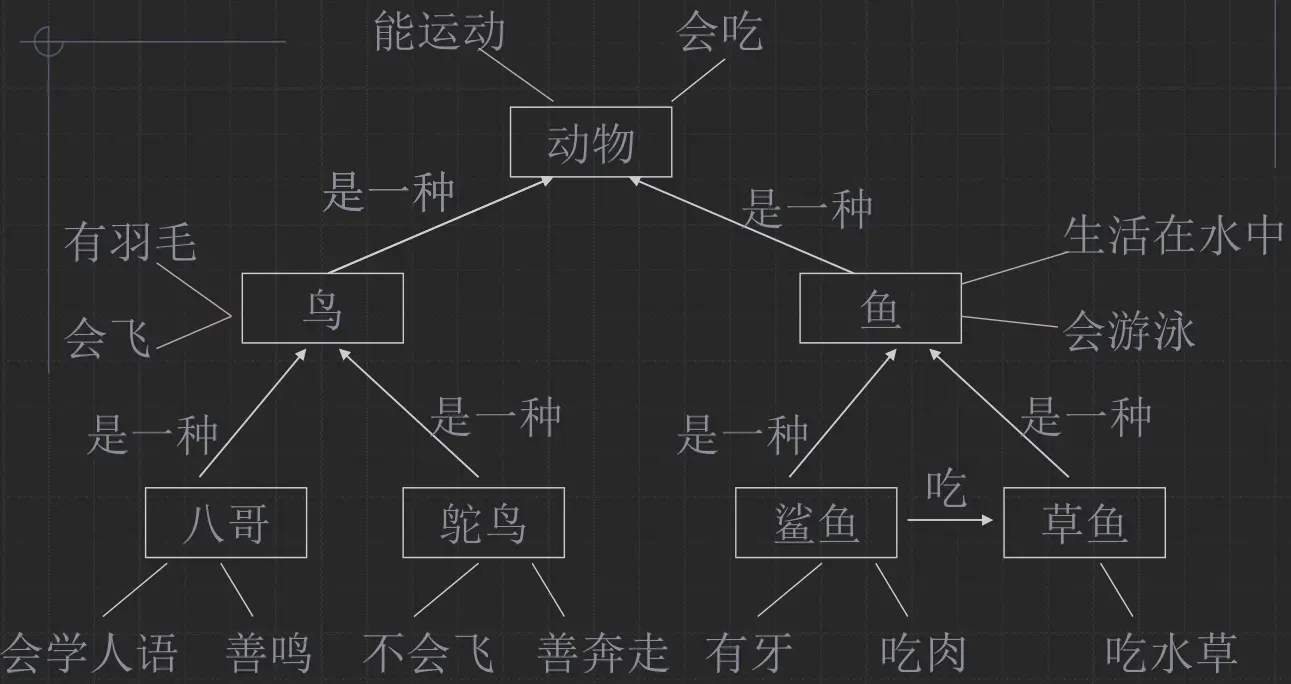
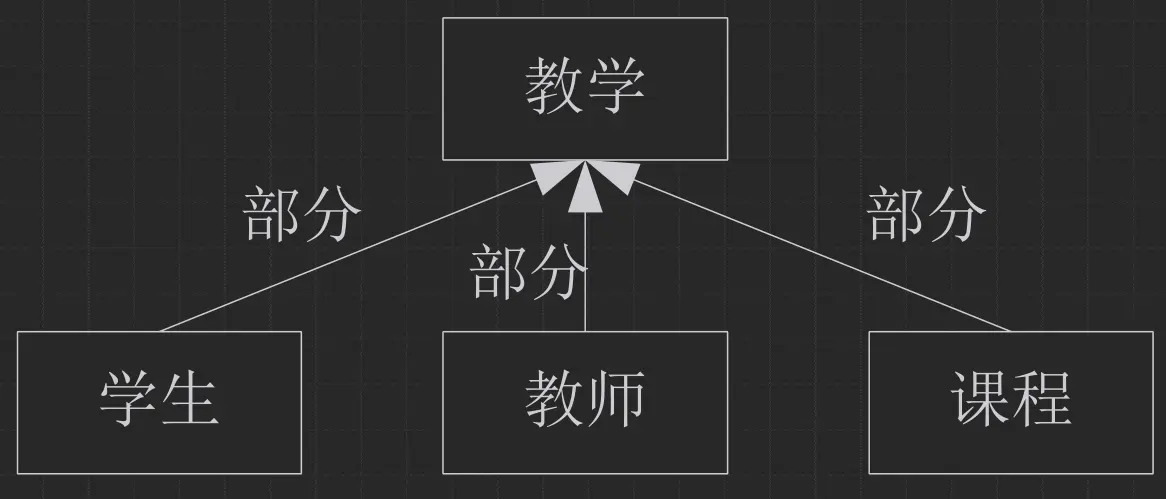
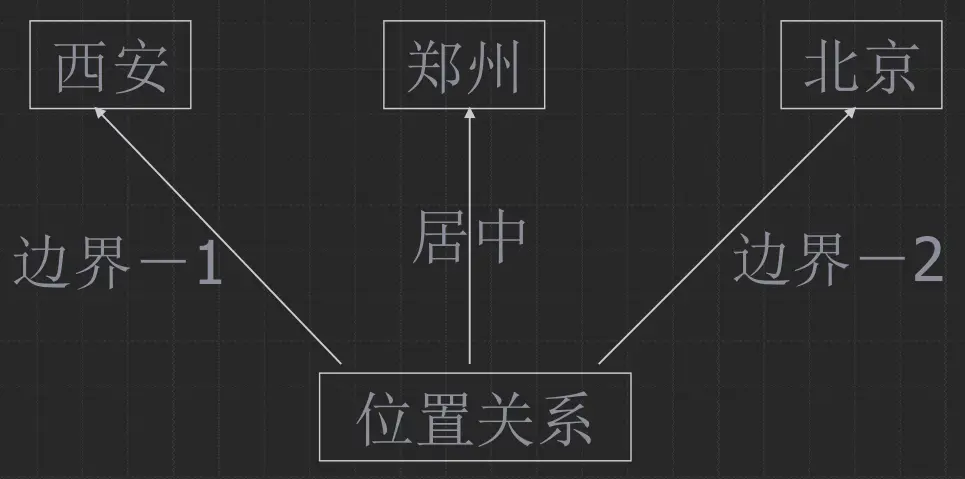
语义网络求解过程

匹配

根据问题构造网络, 其中有些节点或边的标识为空, 表示待求解问题
从知识库中找可匹配的网络
与询问处匹配的则是问题的解

(说的啥玩意)

搜索

采用某种策略, 在知识库中寻找可利用的知识, 从而构造一条代价较小的推理路线, 使问题得到解决的过程

盲目搜索

广度优先
深度优先
有界深度优先
- 迭代加深
- 找到一个解后减少界限, 以找到最优解
代价树广度优先: 到根的代价小优先
代价树深度优先: 当前点到子节点的代价小的子节点优先

代价树的要从图转换成树 (隐试转换, 在搜索过程中体现, 不是建树), 重复的算不同节点, 会增加节点个数

启发式搜索

估价函数 $f(x) = g(x) + h(x)$, $g(x)$ 是根到 $x$ 的实际代价, $h(x)$ 是 $x$ 到终点的估计代价. 可调整二者占比.

$h(x)$ 称为启发函数

A算法: 在图搜索的每一步中都使用估价函数
A* 算法: $g(x) > 0$, $h(x) \le H(x)$, $H(x)$ 为 $x$ 到终点的实际代价.
局部择优: 优先走当前节点的子节点估价最小的
全局择优: 所有可走节点中选择估价最小的

与或树上的搜索

深/广度优先略

min-max 搜索: 略

$\alpha - \beta$ 剪枝

早忘记了, 不学了

搜索的效率和完备性

不学了

经典逻辑推理

按某种策略由已知判断推出另一个判断的思维过程. 在人工智能中, 推理是由程序实现的, 称为推理机.

模式匹配: 对两个知识模式进行比较, 看是否一致或相似.

确定性匹配: (经过变量代换后) 完全一致
不确定性匹配: 两个知识模式不完全一致, 相似程度在规定的限度内

冲突: 多个知识匹配

冲突消解策略: 按照一定顺序排序, 选 “最优” 的一个

变量代换

$\theta = \{t_1 / x_1, t_2 / x_2 , \dots, t_n / x_n\}$, 其中 $x_i$ 是某一公式中不同的变元, $t_i$ 是项 (常量, 变量, 函数等), $t_i$ 不能是 $x_i$, $t$ 的任何子集不能是 $x$ 的任何子集的一个置换. 若 $F$ 为表达式, 则 $F\theta$ 表示对 $F$ 用 $t_i$ 代换 $x_i$ 后得到的表达式, $F\theta$ 称为 $F$ 的特例

复合:

$$\begin{aligned} \theta &= \{t_1/x_1, t_2/x_2, \dots, t_n/x_n\} \newline \lambda &= \{u_1/y_1, u_2/y_2, \dots, u_m/y_m\} \end{aligned}$$

复合代换 $\theta \circ \lambda$ 是从

$$\{t_1\lambda/x_1, t_2\lambda/x_2, \dots, t_n\lambda/x_n, u_1/y_1,u_2/y_2, \dots, u_m/y_m\}$$

中删去如下两种元素:

$$\begin{aligned} &t_i\lambda/x_i, &if\ t_i\lambda = x_i, \newline &u_i/y_i, &if\ y_i\in \{x_1,x_2,\dots,x_n\} \end{aligned}$$

后剩下的元素所构成的集合

$F(\theta \circ \lambda)$ 等价于 $(F\theta) \lambda$

公式集的合一: $F = \{F_1, F_2, \dots, F_n}$, 若存在一个代换 $\lambda$, 使得 $F_1\lambda = F_2\lambda = \dots = F_n\lambda$, 则称 $\lambda$ 是公式集 $F$ 的一个合一, 且称 $F_i$ 是可合一的. 公式集的合一不唯一.

最一般合一 $\sigma$ 是 “不可分解” 的合一, 最一般合一唯一.

求最一般合一: 找出公式集中不同的地方, 用最简单的一个代换将他们变成相同. 这个代换复合进结果代换, 直到公式集唯一, 得到的结果代换就是最一般代换.

自然演绎推理

三段论, 拒取式, CP 等

归结演绎推理

要证明 $P\rightarrow Q (\neg P \vee Q)$ 永真, 只需证明其否定 $\neg (P\rightarrow Q)$ ($P\wedge \neg Q$) 永假.

子句

原子谓词公式及其否定称为文字. 文字的析取式称为子句. 不包含任何文字的子句称为空子句.

子句集是合取范式的项构成的集合. 任何谓词公式都可以通过等价关系以及推理规则化为相应的子句集.

把谓词公式化成子句集:

利用 $P \rightarrow Q \Leftrightarrow \neg P \vee Q$ 消去 $\rightarrow$ 和 $\leftrightarrow$
利用等价关系把 $\neg$ 移到靠近谓词的位置
重命名变元, 使不同量词约束的变元有不同名字
消去存在量词

前面没有全称量词约束, 直接用常元 (自己假定) 替换
前面有全称量词约束, 用关于全称量词变元的函数 (自己假定) 替换

把全称量词移到公式左边
化成主合取范式
消去全称量词
子句变元更名, 不同子句用不同名字
得到子句集

子句集的意义: 谓词公式 $F$ 不可满足的充要条件是其子句集 $S$ 不可满足.

子句集不可满足: 对于任意论域的任意一个解释, 子句不能同时取得真值.

海伯伦域

md不靠

证明任意一个论域很难, 可以在海伯伦域这个特殊的域上进行判定, 与任意论域等价.

海伯伦域 $H_\infty$, 构造方法如下:

$H_0$ 集合包含 $S$ 中出现的所有个体常量; 如果没有则把一个常量 $a$ 放进去. 以 $H_i$ 为定义域,

鲁滨逊归结原理

两个子句, 其中有互补文字, 那么可以把互补文字去掉, 两个放一起析取, 得到的子句称为归结式.

直观理解就是两个互补的总有一个真一个假, 那么两个子句同时满足, 必须其他部分有一个满足的.

推论1: $(S - \{C_1, C_2\}) \cup \{ C_{12} \} \text{不可满足} \Rightarrow S \text{不可满足}$

推论2: $S \cup \{ C_{12}\} \text{不可满足} \Leftrightarrow S \text{不可满足}$

归结得到空子句, 则不可满足

谓词逻辑由于有变元或常元, 不能直接归结. 需要对要消去的互补文字中所有的变元或常元, 使用最一般合一变量代换, 然后才可以归结.

若子句内部有可以合一的文字, 那么应该先用 $\sigma$ 合一. $C\sigma$ 称为子句 $C$ 的因子. 若 $C\sigma$ 为单一文字, 则称为单元因子.

归结反演

要证明 $Q$ 是 $P_1, P_2, \dots P_n$ 的结论, 只需证明 $(\bigwedge P_i) \wedge \neg Q$ 是不可满足的, 即子句集不可满足.

应用归结原理证明定理的过程称为归结反演

用归结原理求解问题

跳过先

归结策略

跳过先

删除: 删除无用的子句缩小归结范围

纯文字

限制: 对子句进行限制, 减小盲目性

遗传算法

编码

串编码, 称为染色体 (个体), 每位称为基因. 通常使用二进制编码

适应度: 将染色体解码, 带入目标函数算得的值

交叉

单点交叉: 染色体中选一个点, 交换两个部分, 得到新的个体
两点交叉: 选两个点, 交换中间

变异

单点变异: 每位基因按照概率改变
对换变异: 随机选取两个位置交换
位移变异: 选取一位移到最前

选择

轮盘赌: 根据适应度, 概率选择
两两竞争: 随机选取两个个体, 选出适应度大的那个
锦标赛选择: 随机选择 S 个个体, 选择适应度最大的
精英保留: 选取最大的

过程

随机生成 $N$ 个个体
选择 $N$ 个放入交叉池 (因为概率问题, 所以可能会选到一样的个体)
按顺序两两组合, 依交叉概率 $p_c$ 交叉, 得到子代
子代所有基因变异概率 $p_m$ 固定, 按变异概率变异
从父代和子代中选择 $E$ 个最好的
从父代和子代中根据选择算子选择 $N-E$ 个, 一共 $N$ 个, 进入下一轮

模糊逻辑

映射 $\mu_A : U \rightarrow [0, 1]$, 为定义在论域 $U$ 上的一个隶属函数

由 $\mu_A(u), u \in U$ 所构成的集合 $A$ 称为 $U$ 上的一个模糊集合

$\mu_A(u)$ 称为 $u$ 对 $A$ 的隶属度

(大概是表示 $u$ “属于” $A$ 的 “程度”)

模糊集合的表示

若论域为有限离散集合:

扎德表示法

$$A = \mu_A(u_1) / u_1 + \mu_A(u_2) / u_2 + \dots \mu_A(u_n) / u_n$$

$+$ 和 $/$ 只是表示方法, 不是运算符号

隶属度为 $0$ 的元素可以不写

向量表示法

$$A = (\mu_A(u_1), \mu_A(u_2), \dots \mu_A(u_n))$$

序对表示法

$$A = \{ (u, \mu_A(u)) \mid u \in U \}$$

若论域为连续集合:

积分表示法

$$A = \int\limits_{u \in U} \mu_A(u) / u $$

积分号和上面的 $+$ 一样, 只是一个表示方法

模糊集合的运算

$$\begin{aligned} A \cup B: \mu_{A \cup B} &= \max\{\mu_A(u), \mu_B(u)\} \newline A \cap B: \mu_{A \cap B} &= \min\{\mu_A(u), \mu_B(u)\} \newline \neg A: \mu_{\neg A} &= 1 - \mu_A(u) \end{aligned}$$

$$A \subseteq B \Leftrightarrow \forall u \in U, \mu_A(u) \le \mu_B(u)$$

$\lambda$ 水平截集

$$A_\lambda = \{u | u \in U, \mu_A(u) \ge \lambda \}$$

为 $A$ 的 $\lambda$ 水平截集, $\lambda$ 称为阈值或置信水平

模糊关系

$R \subset U \times V$

(可以看成一个函数 $R(u, v)$, 在二元逻辑上, $x, y$ 有这个关系, 则 $R(x, y) = 1$, 而在模糊逻辑上, $R(u, v)$ 的值域是 $[0, 1]$, 表示有这个关系的 “程度”.)

用 $\mu_R(u, v)$ 表示隶属度.

矩阵表示和图表示

关系的性质:

自反性: $\mu_R(x, x) = 1$
对称性: $\mu_R(x, y) = \mu_(y, x)$
传递性: $\forall x, y, z \in U, \forall \lambda \in [0, 1]$, $\mu_R(x, y) \ge \lambda, \mu_R(y, z) \ge \lambda$, 有 $\mu_R(x, z) \ge \lambda$

复合关系

$R_1 \in U \times V$, $R_2 \in V \times W$, $R_1 \circ R_2$ 的隶属度为

$$\mu_{R_1 \circ R_2}(u, w) = \max\left\{\min\{\mu_{R_1}(u, v), \mu_{R_2}(v, w)\}\right\}$$

用矩阵表示, 则是矩阵乘法的形式, 把加换成 $\min$, 把乘换成 $\max$

复合运算不满足交换律 (想想矩阵乘法)

等价关系

满足自反性, 对称性, 传递性

定理 $R \circ R \subseteq R$ 是 $R$ 满足传递性的充要条件

$\lambda$ 截矩阵

把 $R$ 矩阵中 $\ge \lambda$ 的设为 $1$, 其他设为 0, 得到的布尔矩阵. 其中划分了两个等价类.

当 $\lambda$ 从 $0$ 上升到 $1$ 时, 分类由粗变细, 构成一个动态的多层次分类, 叫模糊分类

模糊推理

格式:

text

知识: IF x is A Then y is B
证据:    x is A'
----------------------------
结论:                y is B'

或者

text

知识: IF x is A  Then y is B
证据: IF y is B  Then z is C
-----------------------------
结论: IF x is A' Then z is C'

模糊关系构造: 给两个模糊集合 $A, B$, 构造一个关系 $R \subseteq A \times B$.

Mamdani 法
扎德法

(公式都会给出)

不, 非: $\mu_{\text{不} A}(u) = 1 - \mu_A(u)$
很, 非常: $\mu_{\text{很} A}(u) = \mu_A^2(u)$
有些, 稍微: $\mu_{\text{有些} A}(u) = \mu_A^\frac 1 2(u)$

$U$ 是工作成绩 $= \{1,2,3,4,5\}$

$V$ 是工资 $= \{100, 200, 500, 800, 1200\}$

$A$ 和 $B$ 分别是 $U$ 和 $V$ 上的两个模糊集

$A$ 表示工作成绩 “好” $={\(1,0), (2,0.2), (3,0.5), (4,0.8), (5,1)\}$

$B$ 表示工资"高" $=\{(100,0), (200,0.1),(500,0.5),(800,0.6),(1200,1)\}

已知 $R$, 已知 $A’=$ 工作成绩 “非常好” $=[0, 0.04, 0.25, 0.64, 1]$

$B’ = A’ \circ R$

text

知识: IF x is A  Then y is B
证据: IF y is B  Then z is C
-----------------------------
结论: IF x is A' Then z is C'

$C’ = A’ \circ (R_{AB} \circ R_{BC})$

可信度方法

CF 模型

IF E THEN H (CF(H, E))

E: 证据
H: 结论
CF(H, E): 知识的可信度, 称为可信度因子. 取值范围是 $[-1, 1]$

$\ $

CF(H, E) > 0: 证据增加了结论为真的程度, $P(H|E) > P(H)$
CF(H, E) = 1: 证据使结论为真, $P(H|E) = 1$
CF(H, E) < 0: 证据增加了结论为假的程度, $P(H|E) < P(H)$
CF(H, E) = -1: 证据使结论为假, $P(H|E) = 0$
CF(H, E) = 0: 证据和结论没有关系, $P(H|E) = P(H)$

$\ $

CF(E): 证据的可信度, 和上面的类似

组合证据

$E = E_1 \mathrm{AND} E_2 \dots \mathrm{AND} E_n, CF(E) = \min\{CF(E_i)\}$
$E = E_1 \mathrm{OR} E_2 \dots \mathrm{OR} E_n, CF(E) = \max\{CF(E_i)\}$

结论 $CF(H) = CF(H,E) \times \max\{0,CF(E)\}$

不确定性的合成

若根据不同的证据得到不同的结论可信度, 要求总的可信度, 由如下公式合成:

$$ CF(H) = \begin{cases} CF_1(H) + CF_2(H) - CF_1(H) \times CF_2(H) &CF_1(H) \ge 0, CF_2(H) \ge 0 \newline CF_1(H) + CF_2(H) + CF_1(H) \times CF_2(H) &CF_1(H) \le 0, CF_2(H) \le 0 \newline \frac{CF_1(H) + CF_2(H)}{1 - \min\{|CF_1(H)|, |CF_2(H)|\}} & CF_1(H) \times CF_2(H) < 0 \end{cases}$$

神经网络

单层感知器, 就是一个参数待定的线性方程, 加上一个激活函数.

局限性: 无法解决异或等非线性问题

目录

「笔记」人工智能导论

第一章 绪论

定义

发展

研究内容

研究途径

派别

传统三大核心研究内容

应用

知识表示

状态空间

问题归约

谓词逻辑

语义网络

节点表示

语义网络表示

语义网络求解过程

搜索

盲目搜索

启发式搜索

与或树上的搜索

$\alpha - \beta$ 剪枝

搜索的效率和完备性

经典逻辑推理

变量代换

自然演绎推理

归结演绎推理

子句

海伯伦域

鲁滨逊归结原理

归结反演

用归结原理求解问题

归结策略

遗传算法

编码

交叉

变异

选择

过程

模糊逻辑

模糊集合的表示

模糊集合的运算

$\lambda$ 水平截集

模糊关系

复合关系

等价关系

$\lambda$ 截矩阵

模糊推理

可信度方法

不确定性的合成

神经网络

第一章绪论