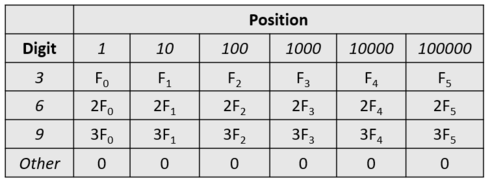
有 $q$ 个询问每次询问的 $k$ 不变, 要求找到 $k$ 个非负数的和为 $n$. 如果这 $k$ 个数中某个数位 (个位, 十位, 百位…) 上有 $3, 6, 9$ 那么就会增加幸运值. 具体的数值如下表, $F$ 都会提前给出, 求出最大幸运值.

$1 \le n, k \le 999999, 1 \le F_i \le 10^9, 1 \le q \le 10^5$

能看出来和应该是一个背包(取一些数, 使其和为某值), 但明显不能直接背包, 因为这样复杂度至少 $O(k^2)$

注意到, 不同数字相同位置的数位交换对答案没有影响, 比如 $31, 29$ 和 $39, 21$ 对答案的贡献是一样的. 利用这个性质, 我们可以把 $k - 1$ 个数都构造成**仅由$0, 3, 6, 9$**组成(因为对答案的贡献为$0$, 所以可以含前导零), 而只剩下一个数, 可能有除 $0, 3, 6, 9$ 之外的其他数字. 也就是说, 能够构造出一种解, 使得最多只有一个数字, 每一位不全为 $0$ 或 $3$ 或 $6$ 或 $9$.

二维平面上有 $n$ 个点$(x_i, y_i)$. 有一辆电汽车, 电池容量为 $W$, 要从点 $s$ 到点 $t$. 每个点都可以充电, 充一个单位的电量需要 $c_i$ 点花费. 一个单位的电量能走一个单位距离. 两个点之间的距离是笛卡尔距离. 开始时车在 $s$ 点电量为 $0$, 问在充电次数不超过 $\Delta$ 的情况下, 到达 $t$ 点的最小花费.

$1 \le n \le 1000, 0 \le x_i, y_i \le 10^6, 1 \le c_i \le 10^4, 1 \le W \le 10^5, 1 \le \Delta \le 10$

首先想到经典贪心题. 确定一条路线, 那么一定是两种选择:

1. 充满电往下走
2. 充到刚好到下一个点

根据这两个决策, 我们设计dp.

$dp(i, x, 0)$ 表示已经充了 $i$ 次电, 当前在点 $x$, 从某个点充到刚好能过来, 即现在的电量为 $0$.

在二维平面上给出 $n$ 个敌军的坐标 $A_i(x_i, y_i)$, 再进行q次强制在线询问:

每次询问将给出一个炮台坐标 $(x_m, y_m)$, 需找出所有能被坐标 $(x_m, y_m)$ 攻击到的敌军的下标. 这里定义炮台 $(x_m, y_m)$ 能攻击到的范围是 $y = y_m \pm \frac{x - x_m}{2}$ 所夹出来的右半部分, 包括边界.

接下来将这些下标按照升序排序, 记为$i_0, i_1, \dots i_k$

计算结果 $(\sum_{j=0}^{k-1} i_j \cdot 5782344^j) \mod 10^9 + 7$, 输出结果.

$1 \le x_i, y_i \le 10^9, 1 \le n, q, \le 10^5$

保证所有查询中被攻击到的敌军总数不超过 $10^6$, 保证$x_i > 0, x_m < 0$

有两种考虑方式.

第一种

施鹏飞学长讲的:

注意到每个炮台所能攻击到的范围角度是固定的, 所以为了更好地刻画炮台 攻击的覆盖范围, 我们可以将炮台的攻击范围投影到$x=0$这条线上; 类似地, 将每个敌军以同样的角度都投影到$x=0$这条线上. 如果两条线段有交集, 那么 该炮台就可以攻击到这个敌军.

$n$ 个长为 $m$ 的不同字符串, 等概率地藏起来一个字符串, 然后游戏者来猜藏起来的串是什么. 每一步游戏者等概率地询问该字符串的某个位置的字符是什么. 不断地知道该字符串的一些位置的字符后, 游戏者就可以确定藏起来的串是什么, 题目要求游戏者的期望步数.

$1 \le n \le 50, 1 \le m \le 20$

这个步数期望的贡献转化没见过, 记下来.

由于期望的线性性质, 我们可以先求猜出某一个的期望步数. 这样乘以 $\frac{1}{n}$ 就是所有的期望步数了.

然后考虑如何求猜出一个串的期望步数.这里转化一下贡献, 把步数拆开, 即变为 $$E’ = \sum_{s \in ALL, |s| = 1}P(s) \cdot 1(\text{走第一步}) + \sum_{s \in ALL, |s| = 2}P(s) \cdot 1(\text{走第二步}) + \dots$$

其中$ALL$是询问集合全集, 即每个位置都询问.

可以发现, 某个字符串对答案有贡献, 当且仅当走第 $k$ 步不能确认.

再根据线性性质, 把询问$s$不能确认的字符串个数加进去, 就有 $$E = \sum_{k=0}^{m} \sum_{s \in ALL, |s| = k}P(s) \cdot \frac{\text{#不能确定的字符串}}{n}$$

有 $n$ 个人, 有些人说真话, 有些人说假话, 每个人都知道所有人是说假话的还是说真话的, 现在问他们每一个人: 说真话的人有多少. 每个人都会给出一个答案. 说假话的人会随便给出[1,n]中的一个数, 但不会给出真实的答案. 现在, 给你两个数 $n, K$, 问你有多少种方案, 能确定恰好有 $K$ 个人说谎. 保证 $n$ 是 $2$ 的幂, 答案模 $777777777$.

$1 \le K \le n \le 2^8, n = 2^p$

假设有 $x$ 个人说真话, 那么会有正好 $x$ 个人给出答案 $x$.

但是会有同时发生的情况 $y$ 个人给出答案 $y$, 这样我们就不能确定到底是 $x$ 个人还是 $y$ 个人说谎了.

所以这种方案不能算.

也就是说, 要求仅有一个数$x$, 满足正好 $x$ 个人给出答案 $x$.

求方案数, 考虑dp.

我们可以用组合数学的思路来想, 有 $n$ 个空, 每个空需要填一个数字, 要求满足有$x$个位置填的是$x$

$dp(i, j, k)$ 表示填入了 $[1, i]$ 个数字在 $j$ 个空中, 其中 $k$ 个人说假话.

用System.Drawing.Graphics的CopyFromScreen()函数即可.

不太懂, 先记着, 大概是调用 user32.dll 里的函数, 参数看不懂