树的序列化

简单介绍树的序列化以及应用

DFS序

遍历树的时候, 在第一次遍历到某个节点的时候入栈, 得到的就是 DFS 序. 入栈可以是节点编号, 也可以是点权.

如:

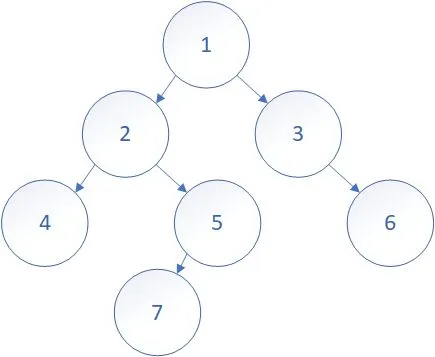
他的 DFS 序是: 1 2 4 5 7 3 6

能够发现, 子树在 DFS 序上是一段连续的区间. 那么怎么确定一棵子树是序列上的哪一段呢? 下面引入 dfn[] 和 out[], 这个 dfn[i] 和 tarjan 算法里的是一样的, 表示节点 i 是第几个访问到的, 如上面这个图的 dfn 是: 1 2 6 3 4 7 5, 而 out[i] 记录的是, 节点 i “退出"时, 当前的 idx 是多少. 如上图的 out 是: 7 5 7 3 5 7 5

把他们放在一起:

dfs 1 2 4 5 7 3 6
i   1 2 3 4 5 6 7
dfn 1 2 6 3 4 7 5
out 7 5 7 3 5 7 5

对于子树 i, 他在 DFS 序上的区间是 $[dfn_i, out_i]$

这样对子树的修改/询问, 就转移到序列上来了.

括号序

第一次遍历到这个节点的时候入栈, 权值为正, 第二次遍历到这个节点退出的时候再入栈一次, 权值为负, 这样得到的序列叫括号序(就像括号一样).

如:

括号序为: +1 +2 +4 -4 +5 +7 -7 -5 +3 +6 -6 -3 -1

(这里为了叙述方便, 假设权值为节点标号)

第一次入栈的点的前缀和, 就是从根到这个点的权值和. 比如节点5, 前缀和是+1 +2 +4 -4 +5, 也就是+1 +2 +5.

找是哪一段区间和上面的差不多, 记录入栈时的 idx 即可.

欧拉序

欧拉序分两类, 第一类就是上面讲的括号序, 第二类先放着, 等学到冯佬的课件再说.