一条路上按顺序有 $n$ 瓶毒药, 对于每个 $i \in [1, n]$, 求出如下的值: 从i出发, 每个时刻都可以向左或向右, 最终可以得到一个吃毒药的排列$P$, 一个排列的伤害定义为$\sum_{j=1}^n D_j \cdot [P_{C_j} = j]$, 求可能的排列中最大的伤害值. $C$和$D$给出.
$2 \le n \le 3 \cdot 10^5$
区间DP显然.
不过这里的状态定义和平常不太一样. 因为要算从每个点走完所有的值, 如果从小区间推到大区间的话, 就要枚举起点, 复杂度$O(n^3)$, 怎么都压不下来.
设$dp(i, j)$为已经走完了区间$[i, j]$, 走完剩下的所有点还需要的最大花费. 转移从大区间推到小区间, 答案就是$dp(i, i) + D_i \cdot [C_i = 1]$.
方程很容易推得:
$$dp(i, j) = max \{ dp(i-1, j) + D_i \cdot [C_{i-1} = j-i+2], dp(i, j+1) + D_j \cdot [C_{j+1} = j-i+2] \}$$
这样复杂度是$O(n^2)$的.
注意到, 对于一个$i$, 最多只可能有种区间的转移会加上$D_i$. 这很好理解, 比如$D_3 = 3$, 那么只有区间$[1, 2]$到$[1, 3]$和$[4, 5]$到$[3, 5]$的这两个走法对应的转移会产生额外的贡献$D_i$, 而其他走到$3$这个点都没有额外的贡献.
如果我们把他放到图上来看, 就会是类似这样的东西:
图
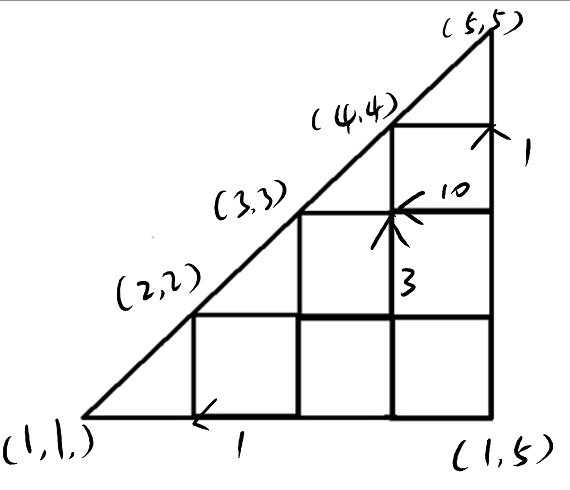
上图是样例. 相当于要求一个从$(1, n)$走到$(i, i)$的最长路(当然最后答案要加上$D_i \cdot [C_i = 1]$). 图中写了数字的边是转移方程中对应的$D_i$, 没有的表示这个转移不加$D_i$.
综上, 最多只会有$2n$条有权值的边, 而没有权值的边, 就直接从下面和右边转移.
于是我们可以根据这个性质进行优化.
考虑维护一颗线段树, 一开始表示第1行的值. 先找当前行横着的有权值的边, 那么这条边左边的点都有可能从这里转移, 所以我们把左边的这个区间每一个点对$dp(i, j) + w$取max, 就得到了所有点的dp值. 如果有两条横着的边, 要注意一下操作的顺序, 要从右往左做, 因为左边的dp值会被右边的更新.
做完一行, 我们就可以轻松单点查询得到一个$(i, i)$的答案了.
然后向上推, 由于竖着的边有权值的可能很少, 所以先假定边权都是0, 那么就是直接对应列相等的点直接转移, 表现在线段树上就是叶子节点的权值不变.
然后考虑有边权的竖直边. 同样是某个点的值可以影响左边区间的值, 如图:
区间更新
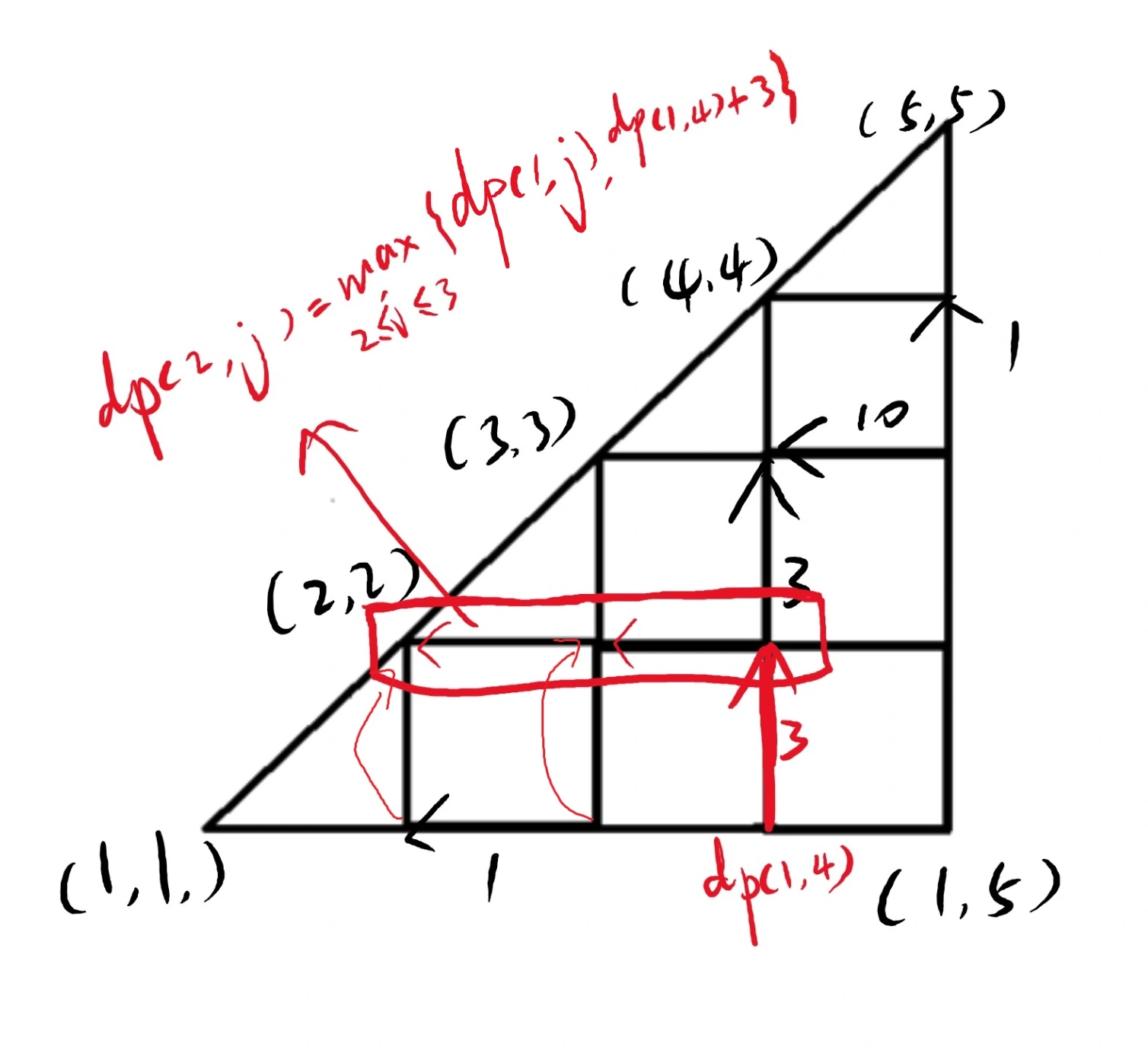
这样就刚好对应了从下面和右边两个点取max.
这个做法就很奇妙……
复杂度$O(n\log n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
|
const int MAXN = 3e5+10;
int n, c[MAXN], d[MAXN];
VI r[MAXN];
struct Node {
int l, r, mid;
LL val, tag;
} tree[MAXN << 2];
void push_up(int u) {
tree[u].val = max(tree[LCH(u)].val, tree[RCH(u)].val);
}
void build(int l, int r, int u) {
tree[u] = {l, r, (l + r) >> 1, 0, 0};
if (l < r) {
build(l, tree[u].mid, LCH(u));
build(tree[u].mid + 1, r, RCH(u));
push_up(u);
}
}
void update_node(int u, LL x) {
tree[u].val = max(tree[u].val, x);
tree[u].tag = max(tree[u].tag, x);
}
void push_down(int u) {
update_node(LCH(u), tree[u].tag);
update_node(RCH(u), tree[u].tag);
tree[u].tag = 0;
}
void update(int l, int r, LL x, int u = 1) {
if (tree[u].l == l && tree[u].r == r)
update_node(u, x);
else {
push_down(u);
if (r <= tree[u].mid)
update(l, r, x, LCH(u));
else if (l > tree[u].mid)
update(l, r, x, RCH(u));
else {
update(l, tree[u].mid, x, LCH(u));
update(tree[u].mid + 1, r, x, RCH(u));
}
push_up(u);
}
}
LL query(int l, int r, int u = 1) {
if (tree[u].l == l && tree[u].r == r)
return tree[u].val;
else {
push_down(u);
if (r <= tree[u].mid)
return query(l, r, LCH(u));
else if (l > tree[u].mid)
return query(l, r, RCH(u));
else
return max(query(l, tree[u].mid, LCH(u)), query(tree[u].mid + 1, r, RCH(u)));
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", c + i);
for (int i = 1; i <= n; i++)
scanf("%d", d + i);
for (int i = 1; i <= n; i++)
if (c[i] > 1 && i - c[i] + 1 <= n)
r[i - c[i] + 1].push_back(i);
build(1, n, 1);
for (int i = 1; i <= n; i++) {
for (int j = r[i].size() - 1; ~j; j--) {
int p = r[i][j];
update(1, p-1, query(p, n) + d[p]);
}
printf("%lld%c", query(i, n) + (c[i]==1) * d[i], " \n"[i == n]);
int j = c[i] + i - 1;
if (j <= n)
update(1, j, query(j, n) + d[i]);
}
return 0;
}
|