多元微分笔记
简单记录, 备忘查找. 考前预习, 考后忘光.
多元函数
极限
以二元函数为例
二元函数的极限成为二重极限
极限存在
以任何方式趋近点$(x_0, y_0)$时, 都有极限且极限都为$A$.
可以构造不同的趋近方式, 如果得到不同的极限, 则说明极限不存在.
eg:
$$f(x, y) = \begin{cases} \frac{xy}{x^2 + y^2}, & x^2 + y^2 \ne 0, \\ 0, & x^2 + y^2 = 0 \end{cases}$$ $$\lim_{(x, y) \to (0, 0)}f(x, y)\text{不存在}$$ $$\because \lim_{(x, y) \to (0, 0), y = kx} \frac{xy}{x^2 + y^2} = \lim_{x\to0}\frac{kx^2}{x^2 + k^2x^2} = \frac{k}{1 + k^2}$$
当 $k$ 取值不同时, 等式右边的值也不同, 所以不存在极限.
连续性
和一元函数一样, 极限存在且极限值等于函数值, 则连续;
如果函数连续, 极限值等于函数值.
多元初等函数在定义域内连续, 且满足有界性, 最大最小值定理, 介值定理, 一直连续性(忘了是啥了).
偏导
对谁求偏导, 就把剩下的看成常量.
点$M_0$处对$x$的偏导几何意义是用平面 $x = x_0$ 截得的曲线对 $x$ 轴的斜率.
高阶偏导
偏导的偏导
混合偏导在偏导连续的条件下与求导次序无关.
初等函数的偏导是初等函数, 初等函数是连续函数, 所以初等函数高阶偏导与求导次序无关.
全微分
$dz = \sum \frac{\partial z}{\partial x_i} dx_i$
可微条件
充分条件: 所有偏导存在且连续
必要条件: 可微偏导必存在
当偏导存在时, 不一定可微, 还要看 $\Delta z$ (即$f(x + \Delta x, y + \Delta y) - f(x, y)$) 与 $\sum \frac{\partial z}{\partial x_i} dx_i$的差是不是$\rho$(即$\sqrt(\sum {x_i}^2)$)的高阶无穷小. 是则可微, 不是则不可微.
故判断一个多元函数是否可微的步骤是:
- 求偏导 $\begin{cases}\text{不存在} &\to \text{不可微} \\ \text{存在} &\to (2) \end{cases}$
- 判断偏导连续 $\begin{cases}\text{连续} &\to \text{可微} \\ \text{不连续} &\to (3) \end{cases}$
- 计算 $\lim_{\rho \to 0} \frac{\Delta z - (f_x \Delta x + f_y \Delta y)}{\rho} = \begin{cases}0 & \to \text{可微} \\ otherwise &\to \text{不可微}\end{cases}$
一些关系
偏导存在与函数连续
偏导存在 $\nrightarrow$ 函数连续
函数连续 $\to$ 偏导存在
可微与偏导存在/连续
可微 $\to$ 偏导存在
偏导存在 $\nrightarrow$ 可微
可微 $\nrightarrow$ 偏导连续
偏导连续 $\to$ 可微
不可微 $\nrightarrow$ 偏导不存在
偏导不存在 $\to$ 不可微
关于全微分和偏导的一些几何理解
偏导$\frac{\partial z}{\partial x}$表示从x轴"引"的一根曲线上x点处函数的变化率, 可以用"切直线"来理解.
微分$dz$是各个方向"引"的曲线上x点处函数的变化率(口胡, 可能是错的, 这么理解一下), 可以用"切平面"来理解.
那么
偏导存在 $\nrightarrow$ 可微
的原因就是偏导只保证了平行于坐标轴的切直线存在, 但是没有保证其他方向上的. 下图就是个例子:
图来自知乎@马同学回答怎么从几何上理解偏导数连续函数必可微?
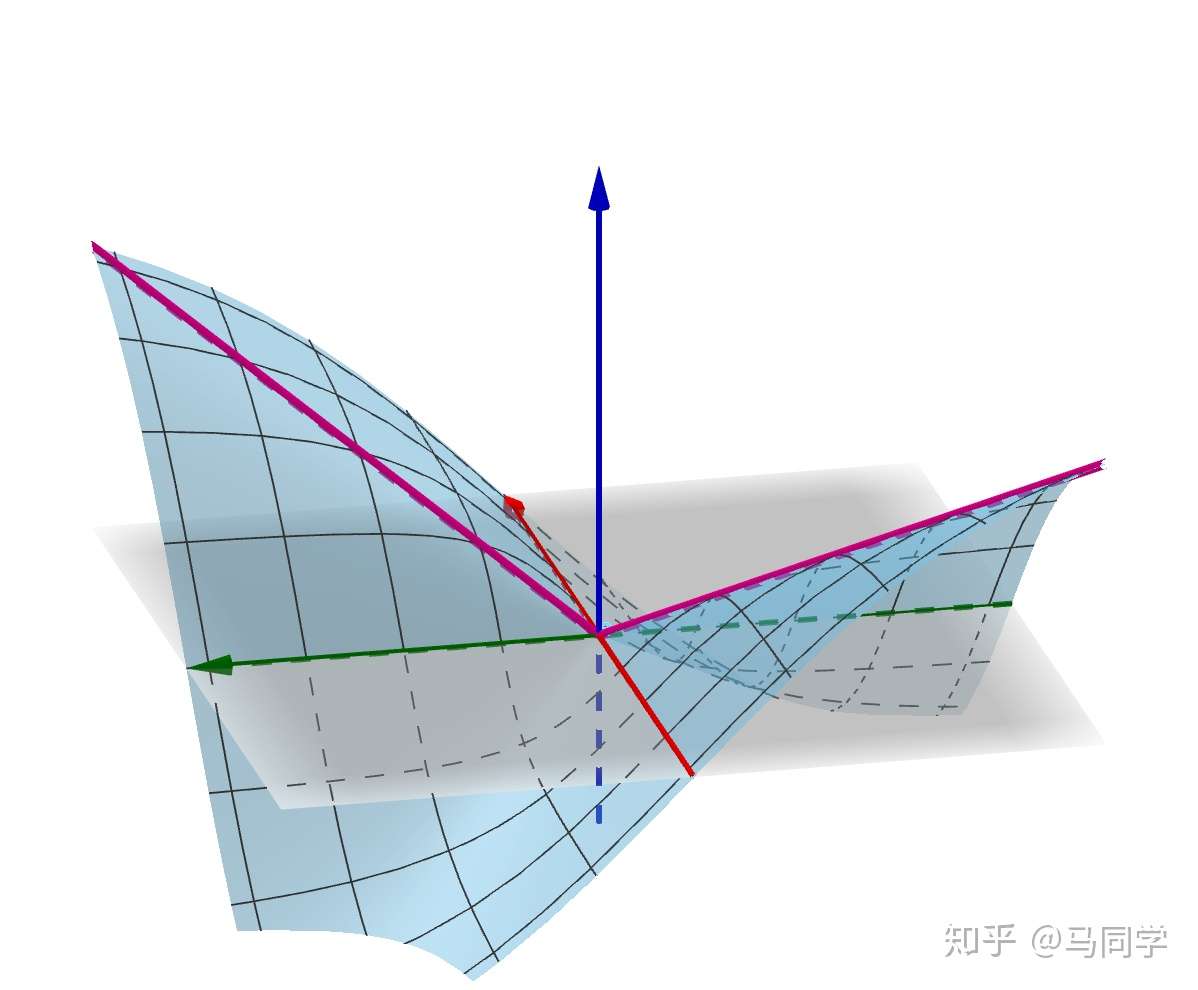
偏导都存在, 但是这个点没有切平面, 不可微
偏导连续 $\to$ 可微
的直观理解如下:
由于偏导连续, 所以在很小的一块区域里可以看成偏导相等.
然后对于邻域中某个偏离两坐标轴的点, 他可以由要求的点经过平行于x轴和y轴"走"过来, 且大小不变, 于是这个点的值可以看成和要求的点的值相同. 每个点都可以这么搞一下, 搞出来不就是一个切平面了吗