一条路上按顺序有 $n$ 瓶毒药, 对于每个 $i \in [1, n]$, 求出如下的值: 从i出发, 每个时刻都可以向左或向右, 最终可以得到一个吃毒药的排列$P$, 一个排列的伤害定义为$\sum_{j=1}^n D_j \cdot [P_{C_j} = j]$, 求可能的排列中最大的伤害值. $C$和$D$给出.

$2 \le n \le 3 \cdot 10^5$

区间DP显然.

不过这里的状态定义和平常不太一样. 因为要算从每个点走完所有的值, 如果从小区间推到大区间的话, 就要枚举起点, 复杂度$O(n^3)$, 怎么都压不下来.

设$dp(i, j)$为已经走完了区间$[i, j]$, 走完剩下的所有点还需要的最大花费. 转移从大区间推到小区间, 答案就是$dp(i, i) + D_i \cdot [C_i = 1]$.

方程很容易推得:

$$dp(i, j) = max \{ dp(i-1, j) + D_i \cdot [C_{i-1} = j-i+2], dp(i, j+1) + D_j \cdot [C_{j+1} = j-i+2] \}$$

有一个长度为$n$的数组$a$, 满足$a_i \in \{0, 1, 2\}$, 你要将其划分成一些连续的区间, 每个区间的长度在$[L, R]$之间, 每个区间的贡献是:

• $-1$: 这个区间的和小于$0$
• $0$: 这个区间的和等于$0$
• $1$: 这个区间的和大于$0$

问最后总的贡献最大是多少

$1 \le L \le R \le n \le 10^6$

显然dp. 设$dp(i)$为前$i$个划分区间的最大贡献, 有

$$ dp(i) = \max_{L \le i-j \le R} \begin{cases} dp(j) + 1, & s_i - s_j > 0 \\ dp(j), & s_i - s_j = 0 \\ dp(j) - 1, & s_i - s_j < 0 \end{cases} $$

($s_i$ 表示$a_i$的前缀和)

朴素转移是$O(n^2)$的, 考虑优化.

从长度为$n$的序列$a$中取一些数, 要求两两满足倍数关系. 问最多取多少个数.

$1 \le n \le 2 \cdot 10^5, 1 \le a_i \le 10^7$

考虑dp, $dp(x)$表示取出来的数不超过$x$ 且一定取$x$, 最多能取的数量. ($10^7$的数组能开)

方程

$$dp(x) = cnt(x) + \max_{y | x} dp(y)$$

其中$cnt(x)$是$x$在$a$中出现的次数.

这可能就是一个"倍数关系转移"的思想吧, 这种题碰到的少, 要牢记.

$O(MAXA\log MAXA)$比较极限.

用类似埃筛的方法转移:

一个 $n \times n$ 的棋盘上会有 $m$ 次变化, 每次变化都会在某个空的位置上出现一个兵 或者 移去存在棋盘上的某个兵. 一个兵处于坐标 $(x, y)$ 可以移动到 $(x, y + 1)$, $(x − 1, y + 1)$ 或 $(x + 1, y + 1)$, 前面是列, 后面是行. 有一个特殊列 $k$, 每次变化, 你都要计算把所有的兵移动到第 $k$ 列(不可以重叠), 需要在棋盘上第 $n$ 之后额外添加的最少行数.

$1 \le n, m \le 2 \cdot 10^5, 1 \le k \le n$

首先把棋子都用最近的移动方式移动到第 $k$ 列, 可让他们重叠在一格里. 这样就变成一维的问题了.

考虑这个一维的序列, 如图, 我们需要把多的兵往下移.

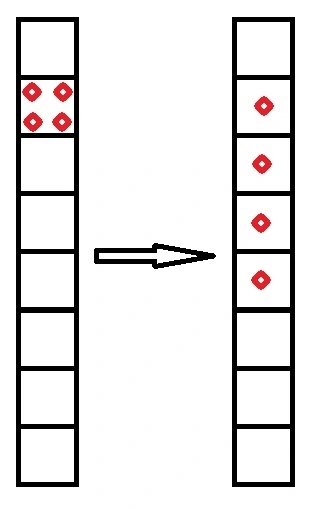
我们记录这个点的权值为当把所有兵依次往下放, 走的最远的那个兵的行号. 图中即 $w(2) = 5$.

设$f(x)$为$x$二进制下$1$的个数. 给出长度为$m$的$01$序列$a$, 给出$L$, 求有多少个$x \in [0, L]$, 满足$f(x + i) \mod 2 = a_i$

$1 \le m \le 100, 0 \le L \le 10^{18}$

设$g(i) = f(i) \mod 2$

我们把$g(i)$求出$[0, L+m]$个, 排成一排, 然后就类似于字符串匹配一样统计个数.

注意到$L$很大, 我们没办法把这个序列全部求出来. 所以这个序列一定有规律.

注意到, 当$i \in [2^{k-1}, 2^k)$时, 有$f(i + 2^k) = f(i) + 1$, 也就是相当于$i$的二进制下的第$k$位从$0$变成$1$, 所以有$g(i + 2^k) = g(i) \oplus 1$. 这样, 我们就发现了序列$g$的构造方式:

第一个是0, 然后把当前序列取反, 拼在后面. 如下:

0
01
0110
01101001
0110100110010110
...

还注意到 $m$ 很小, 只有$100$, 而$2^7 = 128$. 所以我们可以先构造出$g$的前$128$位, 更大的数一定会包含这个序列多次. 用$h(i)$表示$g$的前$2^i$位的序列, $h’(i)$表示$h(i)$每一位取反的序列.

给你一个$n \times m$的01矩阵, 初始全0, 支持四种操作:

1. 将 $(i,j)$ 变成1
2. 将 $(i,j)$ 变成0
3. 将第 $i$ 行的数字全部零一翻转
4. 回到第 $k$ 次操作后的状态

进行 $q$ 次操作, 每次操作后输出当前矩阵1的个数

$1 \le n, m \le 10^3, 1 \le q \le 10^5$

有回到 $k$ 次操作, 考虑可持久化数据结构.

对一个序列可持久化可以用主席树, 对一个矩阵就不好搞了.

把每一行用bitset存一下, 就变成序列了.

bitset.count() 返回1的个数, bitset.flip() 反转.

因为 bitset 要指定大小, 就会出现指定的大小大于$m$的情况, 翻转以后只能考虑后一段, 此时直接 count() 显然错误. 可以用一个后 $m$ 位全1的bitset去与一下反转以后的bitset.

复杂度$O((n + k) \log n)$

给出两个字符串$s_0, t$, 其中$|s_0| \le 100, |t| \le n$. 设$s_{i+1} = s_i + t_i + s_i$, + 表示字符串连接. $q$ 个询问, 形如 k sq, $k$是整数, $sq$ 是非空字符串, 表示询问 $s_k$ 中, $sq$ 的出现次数.

$k < n \le 10^5, q \le 10^6$

首先注意到, $sk$ 的长度是指数爆炸的, 所以不能完全构造出来.

但是 $sq$ 比较短, 我们可以构造出长度恰好大于等于 $sq$ 的$skk$. 注意到 $|skk| \le 2|sq| + 1$这样的话可以在 $O(2|sq|)$ 内求出 $sq$ 在 $skk$ 中出现了几次. KMP或者hash都能做.

$s_{kk+1} = skk + tkk + skk$, 会发现, $skk$已经算过了, 要计算的就是**包含$tkk$**的字符串中, $sq$ 出现的次数.