给出两个字符串$s_0, t$, 其中$|s_0| \le 100, |t| \le n$. 设$s_{i+1} = s_i + t_i + s_i$,
+表示字符串连接. $q$ 个询问, 形如k sq, $k$是整数, $sq$ 是非空字符串, 表示询问 $s_k$ 中, $sq$ 的出现次数.$k < n \le 10^5, q \le 10^6$
首先注意到, $sk$ 的长度是指数爆炸的, 所以不能完全构造出来.
但是 $sq$ 比较短, 我们可以构造出长度恰好大于等于 $sq$ 的$skk$. 注意到 $|skk| \le 2|sq| + 1$这样的话可以在 $O(2|sq|)$ 内求出 $sq$ 在 $skk$ 中出现了几次. KMP或者hash都能做.
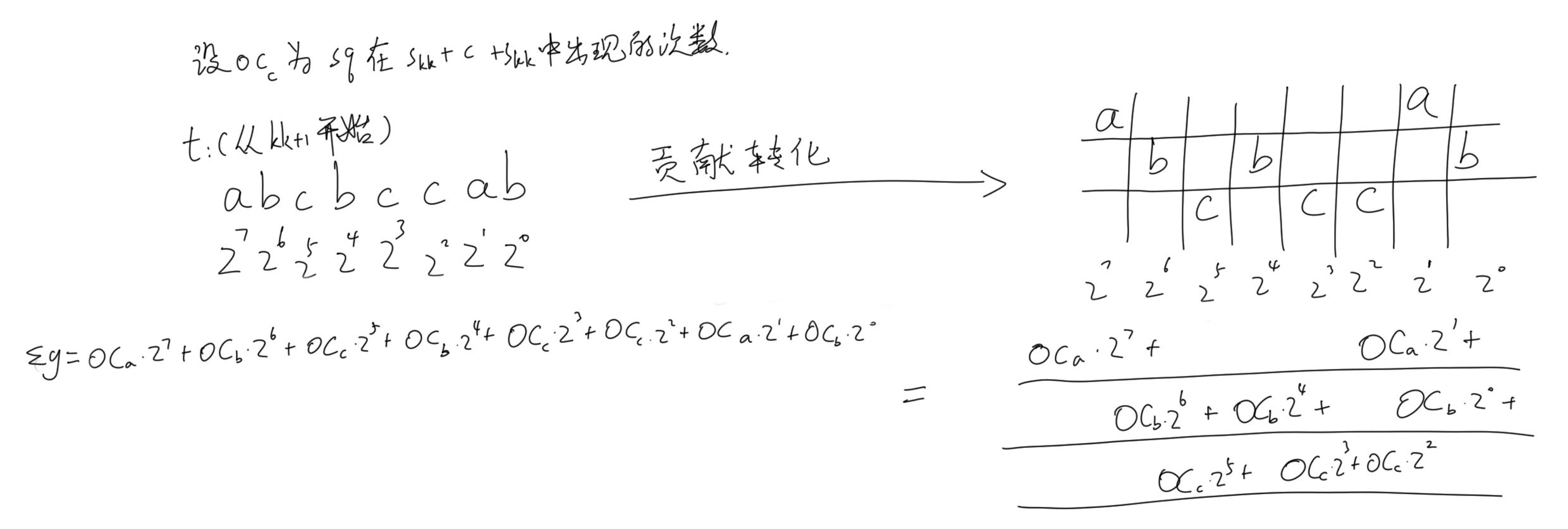
$s_{kk+1} = skk + tkk + skk$, 会发现, $skk$已经算过了, 要计算的就是**包含$tkk$**的字符串中, $sq$ 出现的次数.
以前没学会, 现在感觉好简单啊. 可能是冯佬讲得太好了.
还没理解透彻, 边记着.
在张主席和冯佬的解答下, 应该理解透彻了吧…
$n$个点$m$条边的无向图, 带边权. 定义路径的某种长为 路径上边权的和 - 路径上最大边权 + 路径上最小边权. 求 1 到 其他点的这种路径最小长度.
$2 \le n \le 2 \cdot 10^5, 1 \le m \le 2 \cdot 10^5$
拆点, 分层. 把一个点拆成4个, d[u][0][0] 表示没有走最小值或最大值, dp[u][0][1] 表示没有走最小值而走了最大值, dp[u][1][0] 表示走了最小值没有走最大值, dp[u][1][1] 表示走了最小值和最大值. 每层内的边权就是原来的边权, 并且是双向边; 而跨层的边权需要修改一下, 并且是单向边.
$00 \to 01, 10 \to 11$, 边权为$0$, $00 \to 10, 01 \to 11$, 边权是原来的两倍.
然后跑最短路.
由于最短路的性质和题目的特殊性质, 跑出来一定是减去最大值, 加上最小值的, 否则不是最短路.
分层图的话不用显式建图, 否则不仅很麻烦, 而且很难知道当前点有没有跑最大或最小. 用一个三元组(u, 0/1, 0/1)表示, 既方便了许多, 也能和 d[u][0/1][0/1] 对应. 同时记得 vis 也要写成这种形式.
$n$个人坐在一圈玩游戏, 分别标号$1 \sim n$. 初始每人手里有$k$张牌($2|k$). 一次洗牌, 每个人都会进行这样的操作: (当前手牌设为$x$)把 $\lfloor\frac{x}{2}\rfloor$ 张牌给左边的人, 把 $\lceil\frac{x}{2}\rceil$ 张牌给右边的人.
然而, 人群中有一个🤡, 每次他只会把所有牌给右边的人.
? p用来询问当前局面, $p$ 号玩家有几张牌.每次询问后都进行一次洗牌.
任务是用不超过 $1000$ 次询问, 找出🤡,
! p用来回答找到的🤡.$4 \le n \le 10^5, 2 \le k \le 10^9, 2 | k$
手玩可以发现, 🤡的牌数永远是 $k$, 而且在前 $\frac{n}{2}$ 次洗牌中, 🤡左边的人的牌比 $k$ 少, 右边的比 $k$ 多.
为什么要限制 $\frac{n}{2}$ 呢? 首先, 我们能用的询问很少, 根本到达不了 $\frac{n}{2}$, 所以可以直接假定就是前 $\frac{n}{2}$ 步. 其次, 大于这个数的时候, 就会出现少的和多的交换的情况, 这里不好处理, 我们就不处理.
证明一下:
$n$ 个连续的格子, 从左到右分别标号为 $1 \sim n$. 初始第 $i$ 个格子上的数为 $a_i$. 把从任意一点开始, 正好走 $k$ 步的一条路径成为合法路径. 每一步只能走相邻的格子, 且不能出界. 一条路径的价值是, 每一次走到一个格子, 价值就加上格子上的这个数.
给出$q$个修改, 每次只修改一个格子的数$a_i$, 输出每次修改后的所有路径价值之和模$10^9 + 7$.
$1 \le n, k, le 5000, 1 \le q \le 2 \cdot 10^5, 1 \le a_i \le 10^9$
显然要转化贡献. 这道题也难在转化贡献.
首先有一点很容易想: 我们要求第$i$个位置对所有路径的贡献$cnt_i$, 答案就是$\sum ai \cdot cnt_i$.
接下来, 如果用一条路径上出现的$i$个数求$cnt_i$, 就得用三维dp, 复杂度爆炸. 所以不能这么做.
再转化一次贡献, 求经过了第$i$个位置的合法路径有多少条. 由于一条路径可能不止一个, 所以我们再拆分一下. 设 $A_{i, j}$ 为 第 $j$ 步在 $i$ 的路径条数. 然后求和 $cnt_i = \sum_{j = 0}^k A_{i, j}$.
我从哪里来?
要到哪里去?
